Introduction to Data Science.

Chapter 1: Geo Maps

Few chapters back we already peeked at the human development index data. Now, let's see if clustering the data presents any new, interesting findings. We will attempt to visualize these clusters on the geo map.

Orange comes with a geo add-on, which we will need to install first. Add-ons can be found in the menu under Options. Here we need to select a checkbox for the Geo add-ons. Clicking on the Ok button, the add-on will install, and Orange will restart.

In the toolbox, we now have another group for Geo widgets.

The human development index data is available from the Datasets widget; we can type "hdi" in the filter box to quickly find it. Double clicking the line with the data set loads the data. Before doing anything else we should to examine it in the Data Table.

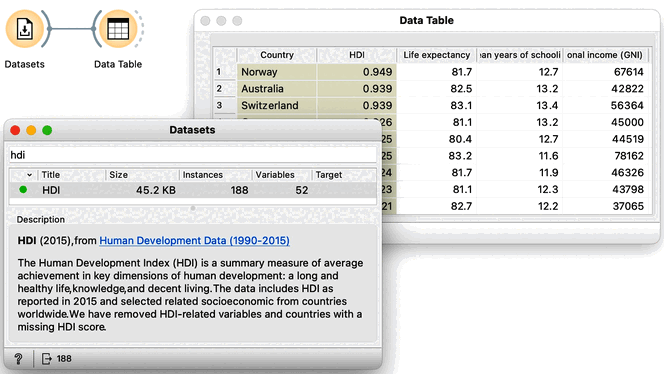
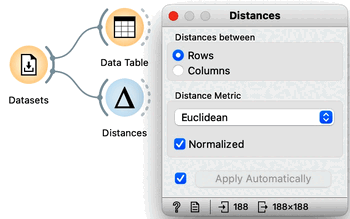
This data includes 188 countries that are profiled by 52 socioeconomic features. To find interesting groups of countries, we first compute the distances between country pairs. We will use the Distances widget with Euclidean distance and make sure that features are normalized. As this data set includes features with differing value domains, normalization is required to put them on a common scale.

In hierarchical clustering, where we add the Hierarchical Clustering widget to the workflow, we will use the Ward method for linkage and label the branches with the names of the countries. Ward method joins the clusters so that the data variance in the resulting cluster is decreased and often produces dendrograms with more exposed clusters.

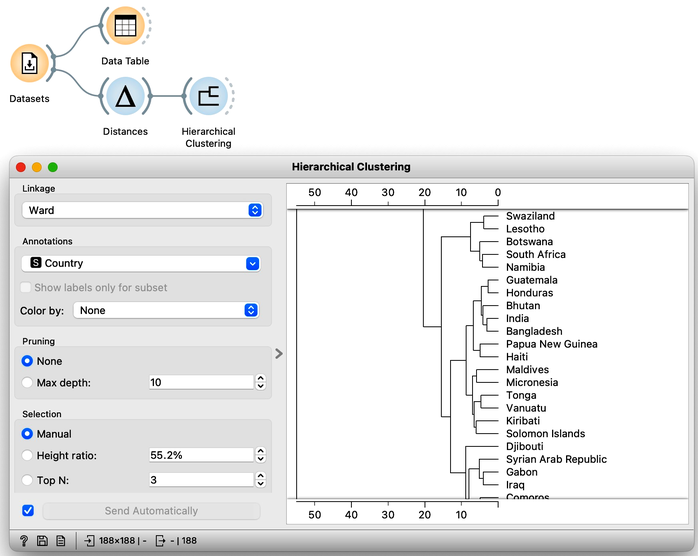
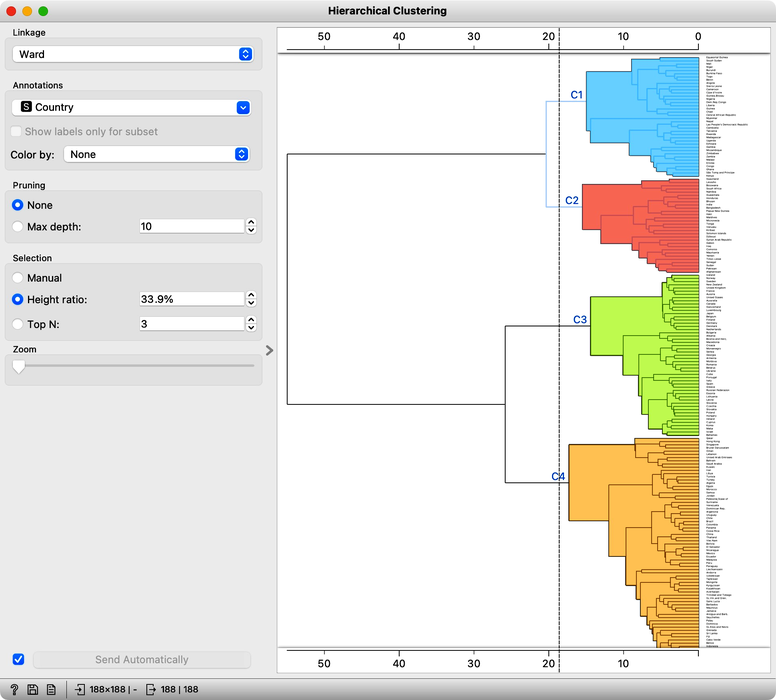
Our clustering looks quite interesting. We see some clusters of African countries, like Swaziland, Lesotho, and Botswana. We also find Iceland, Norway, and Sweden grouped together. And some countries of the ex-Soviet Union. Try to find each of these groups in the dendrogram! By zooming out the dendrogram we can find such a cut that will group the countries into, say, four different clusters.

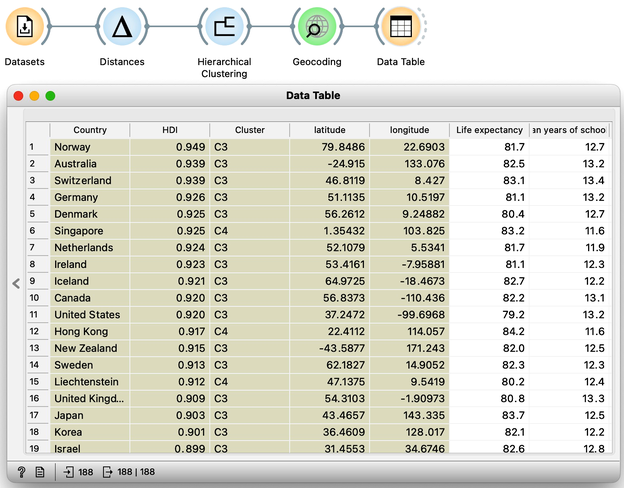
Let us take a look at these four groups on the geo map. To do this, we first need to add the Geocoding widget to the output of Hierarchical Clustering. The widget is already set correctly to use the country name as an identifier. By adding the Data Table we can double check the result and find that every row now includes extra information on the Cluster, which comes from the Hierarchical Clustering widget, and information on the latitude and longitude of the country, added by Geocoding.

We will pass this data on to the Choropleth Map, change the attribute for visualization to Cluster, and the aggregation to Mode. Also, check that Latitude and Longitude are read from the variables of the same name, and that Detail is set to the minimum level.

Well, here it is. The countries of our world clustered!

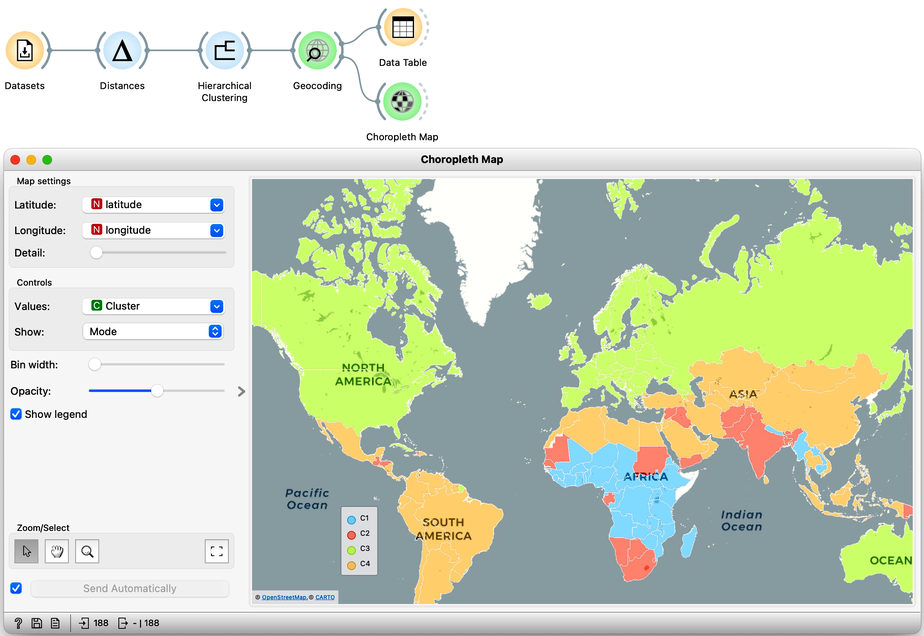
Looks interesting. What we refer to as developed countries are in one cluster. Countries in South America are clustered with some countries in Asia. And we also find a band of sub-Saharan African countries.

It is fascinating that although the data did not explicitly encode any geo-location information, the clusters we found were related to the country's geographical location. Our world really is split into regions, and the differences between countries are substantial.

Did we say "the differences"? So far, authors of this text did an abysmal job of explaining what exactly these clusters are. That is, what are the socioeconomic indicators that are specific to a particular cluster? Are some indicators more characteristic of clusters than others? Which indicators characterize clusters best? So many questions. It is time to dive in into the trick of cluster explanation.

Chapter 2: Explanations

Hierarchical clustering, the topic of our previous chapters, is a simple and cool method of finding clusters in our data. Let us here refresh what we have learned on the course grades example from our previous chapters. The course grades data includes 16 students and seven school subjects. We measured the Euclidean distance between each pair of students and clustered the data accordingly. Let us use the Ward minimum variance method for linkage. This will join clusters so that the points in the resulting cluster are nearest the center. It is a bit more complicated than that, but the idea of Ward linkage is that the points in the resulting clusters are as close together as possible. Below is the workflow and the result of the clustering.

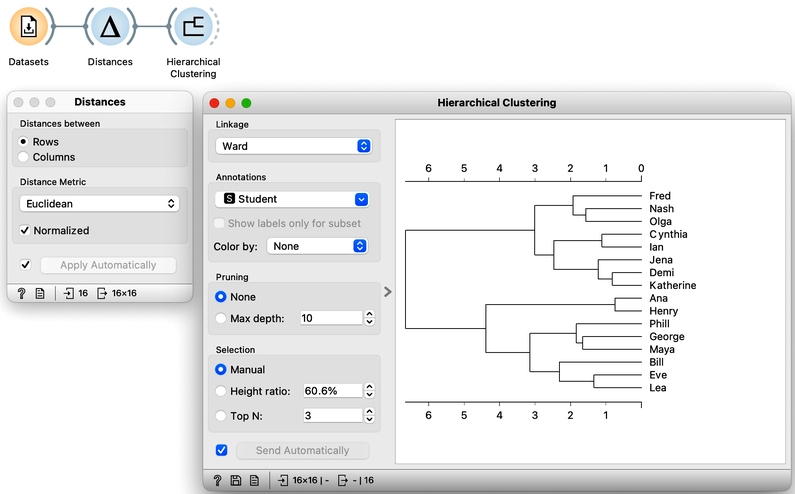
Our problem here, however, is not a clustering algorithm but how to interpret the resulting clustering structure. Why are Phill, Bill, and Lea in the same cluster? What do they have in common?

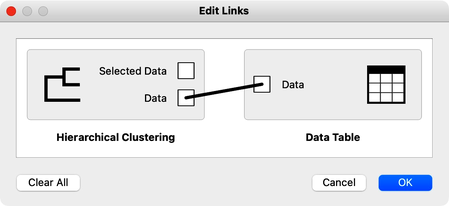
The hierarchical clustering widget emits two signals. Selected data as well as the entire dataset with an additional column that indicates the selection. Let me first show this in the Data Table widget. First, I will select a cluster with Phill, Bill, and Lea, and rewire the connection between Hierarchical Clustering and Data Table to communicate the entire data set. The Data Table now includes the "selected" column, that shows which data items, that is, which students were selected in the Hierarchical Clustering. Fine: Phill, Bill and Lea are among selected ones.

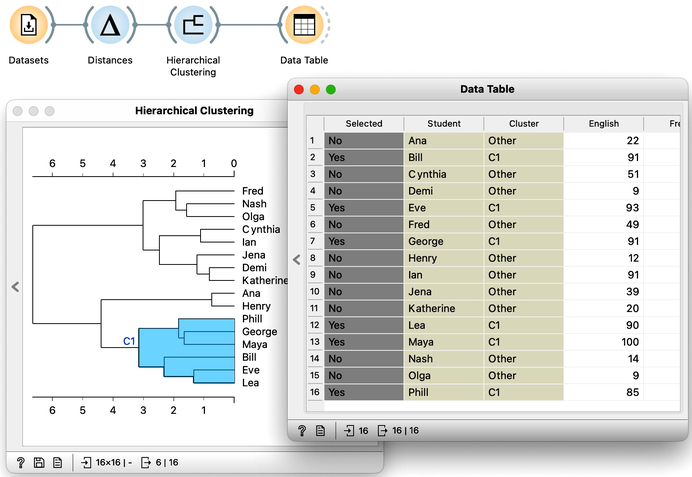
We would now like to find the features, that is, school subjects, which can differentiate between selected students and students outside the selection. This is something we have already done in our chapter on data distribution, where we constructed a workflow that told us which socioeconomic features are related to extended life expectancy? The critical part to remember is that we used Box Plot. Let us add one to the output of Hierarchical Clustering and rewire the signal to transfer all the data instead of just a selection. In the Box Plot widget, I have to set “Selected” as a subgrouping feature, and I also check “Order by relevance to subgroups”.

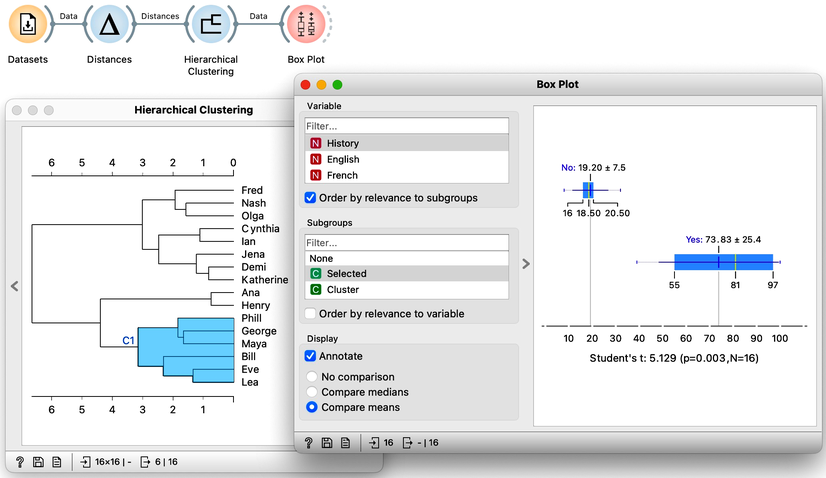
We find History, English, and French at the top of the list of variables. Taking a closer look at History, for example, we can see that Phil, George, and company perform quite well, their average score being 74. Compare that to the mediocre 19 of everyone else. In English, the cluster’s average score is even higher, at 92 compared to the 32 of everyone else. And the scores in French tell a similar story.

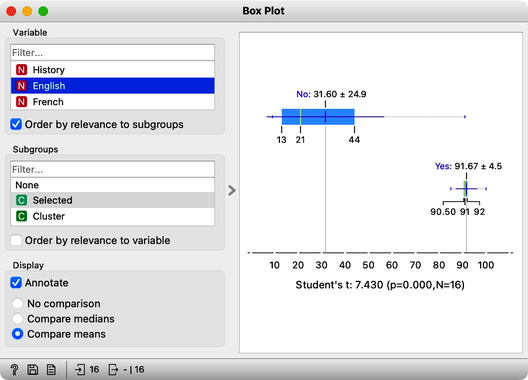
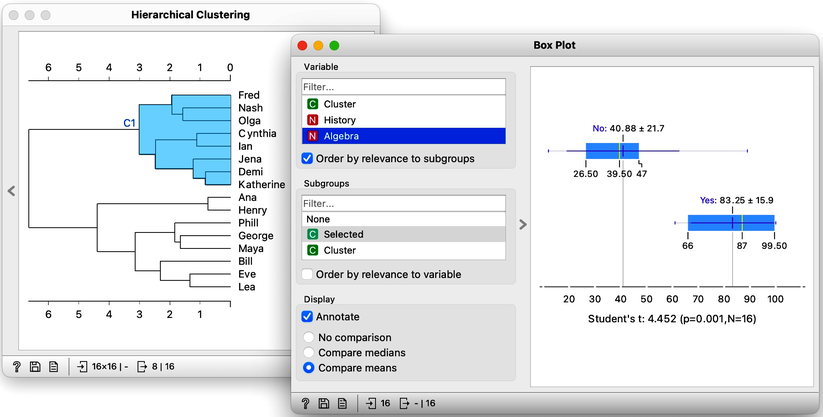
The cluster of students we have selected is particularly good in subjects from social sciences. How about a cluster that includes Fred, Nash, and Katherine? Their scores in History are terrible at 16. However with a score of 83, they do well in Algebra and are better than the other students in Physics. It looks like we have a group of natural science enthusiasts.

The only remaining cluster is the one with Ana and Henry. They love sports.

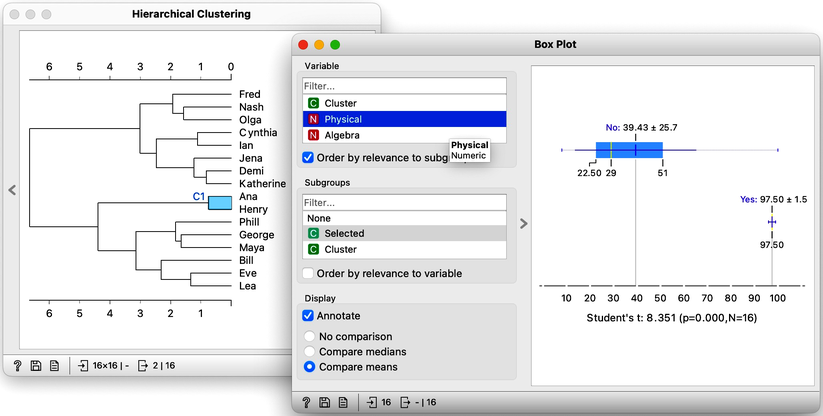
With the Hierarchical Clustering-Box Plot combination, we can explore any cluster or subcluster in our data. Clicking on any branch, will update the Box Plot, which, with its ordered list of variables, can help us characterize the cluster. Box Plot uses the Student’s t statistic to rank the features according to the difference between their distribution within the cluster and distribution of feature values outside the cluster. For instance, the feature that best distinguishes students in my current cluster is Biology, with a Student’s t statistic of 5.2.

Explaining clusters with Orange’s Box Plot is simple. We find it surprising that it was so easy to characterize groups of students in our data sets. We could use the same workflow for other data sets and hierarchical clusters. For instance, we could characterize different groups of countries we found from the socioeconomic data sets. But we will leave that up to you.