Umetna inteligenca za učitelje
Prijazen uvod v analizo podatkov, umetno inteligenco in program Orange
Običajen učitelj ima, vsaj načelno, rad predmet, ki ga poučuje. In kadar mu razposajeni učenci, nadležni starši in, predvsem, neskončna nesmiselna birokracija ne izpijejo vse volje do življenja, si želi to ljubezen prenesti tudi na učence. Navsezadnje ni na svetu nič bolj zanimivega kot opazovati, kako se od tretjega stoletja manjša število prebivalcev rimskih mest, kako iz genskih sekvenc rekonstruirati rodbinsko drevo sevov Covid-2, kako razlikovati med Monetom in Manetom, razmišljati o posledicah meje med avstrijskim in ogrskim delom imperija na razlike med Prekmurci in Prleki ter opazovati, kako teža nihala ne vpliva (res ne vpliva?!) na njegovo periodo.
Gornji primeri niso natreseni kar tako: vseh se lahko lotimo tako, da naberemo primerne podatke in pustimo učencem, da sami odkrijejo, kje in kako se je začel podirati stari Rim ali kdo — Monet ali Manet — slika vodne motive. Učitelj za to seveda potrebuje primerno znanje: znati mora odpreti primeren program, v njem preobrniti podatke, narisati sliko ali izpisati tabelo. In vse to pokazati učencem. Ni težko, verjemite. Samo malo se je treba usesti in pogledati.
V priročniku uporabljamo program Orange: prijazen je, preprost in lep ter ima vse, kar potrebujemo in še veliko več. Deluje na vseh operacijskih sistemih, v slovenščini, pa še zastonj je. (Razkritje: razvija ga - in to že dvajset let - ista skupina kot Pumice). Uporabljati se ga bomo naučili mimogrede, v prvih poglavjih. Kasnejša pa bodo vedno manj o njem in vedno bolj zares o umetni inteligenci in analizi podatkov.
Poglavje 1: Ugrizni v pomarančo
... v katerem prvič odpremo Orange, izvemo, kaj so gradniki in spoznamo idejo njihovega povezovanja
Ko odpremo Orange in zapremo pozdravno okno, se znajdemo pred (večinoma) praznim oknom. Na levi strani je predalnik z različnimi gradniki, ki jih postavljamo na desni del, platno (canvas), kjer jih povezujemo med seboj.
Če se nam zdi, da predalnik zavzema preveč prostora, ga lahko skrijemo oziroma skrčimo: pritisnemo na (komaj vidno) dvojno puščico levo zgoraj nad predalčki.
Če desno-kliknemo na platno, se pokaže menu z nekaj gradniki. Začnemo tipkati ime, del imena ali ključno besedo in izbor gradnikov se oža. Tule bomo potrebovali gradnik Zbirke podatkov, torej tipkamo »zbi...« in ko ugledamo želeni gradnik, kliknemo nanj.
Na poprej praznem platnu se zdaj pokaže ikona z gradnikom. Dvokliknemo nanjo.
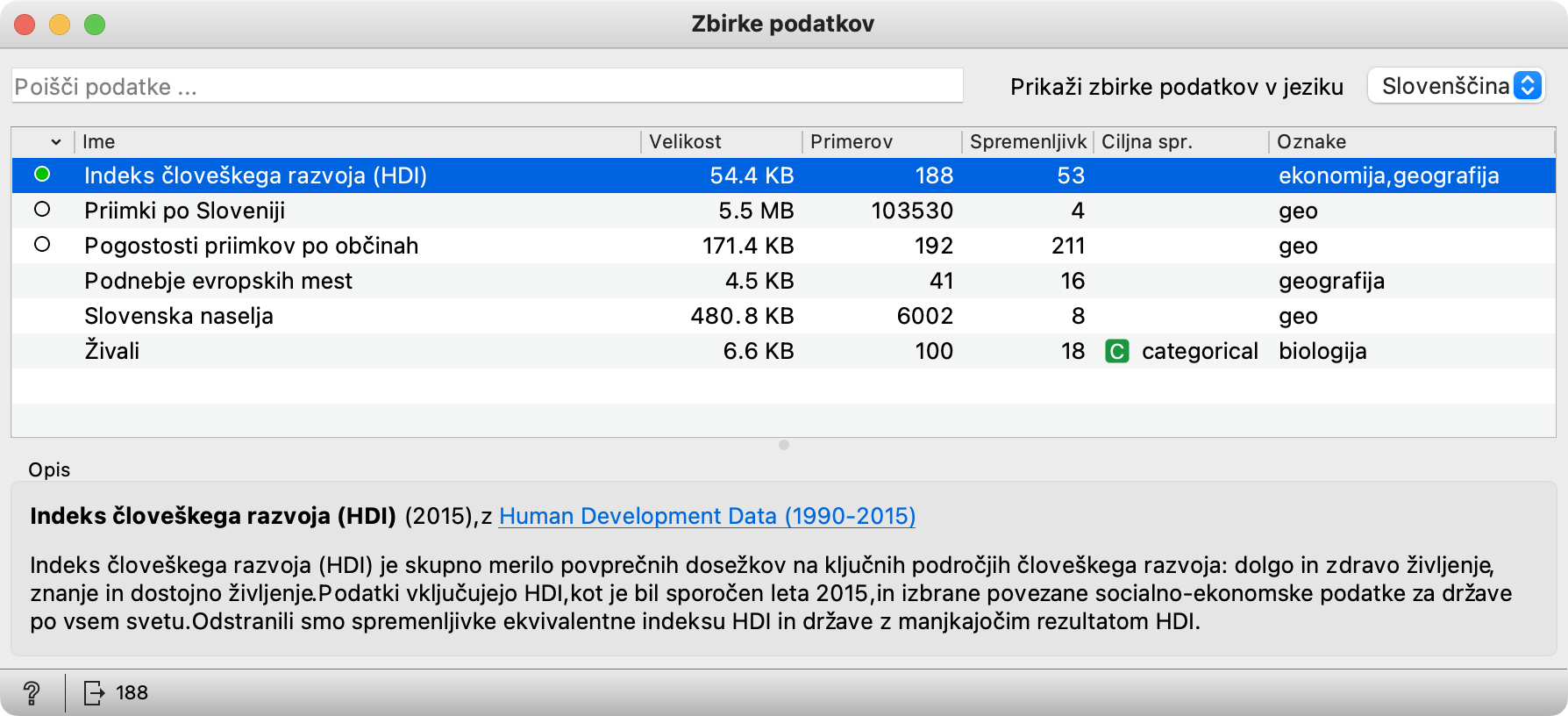
Gradnik Zbirke podatkov nalaga že pripravljene podatke s spletnega strežnika. Svoje podatke, recimo iz Excela, pa naložimo z gradnikom Datoteka (File). Več o tem v dokumentaciji Orange.
Z gradnikom Zbirke podatkov naložimo vnaprej pripravljene zbirke podatkov. Tule kaže podatke v slovenščini, večinoma namenenjene za aktivnosti, ki so predstavljene pri projektu Pumice. Veliko več jih dobimo, če zgoraj desno zamenjamo jezik. Če vemo ime zbirke podatkov, ga lahko vtipkamo v iskalno polje: po štirih vtipkanih znakih bo gradnik ignoriral nastavljene filtre.
V tem priročniku bomo premetavali podatke o Indeksu človeškega razvoja, ki jih zbira Svetovna banka (brez skrbi, ni tako dolgočasno, kot je slišati, sploh ne). Dvokliknimo vrstico s temi podatki, pa jih bo gradnik prebral s spleta.
In zdaj? Kje so, kje jih lahko vidimo?
Za to potrebujemo nov gradnik. Tabela. Dodamo ga tako kot Zbirke podatkov. Dvokliknemo nekam na platno, po možnosti malo desno od Zbirke podatkov, natipkamo začetek imena in izberemo gradnik v menuju. Dvokliknemo novi gradnik na platnu in … razočaranje. Nobene tabele. Pa še pravi, da »Ni podatkov«. Seveda, nima jih. Podatke ima gradnik Zbirka podatkov. Da jih bo lahko dal tabeli, ju moramo povezati.
Gradniki imajo antene; večina dve, nekateri - med katerimi je tudi Zbirka podatkov - le eno. Antene so namenjene prenosu podatkov: z miško povežemo izhodno (in edino) anteno Zbirke podatkov s Tabelo.
 Pokaži ponovno
Pokaži ponovno
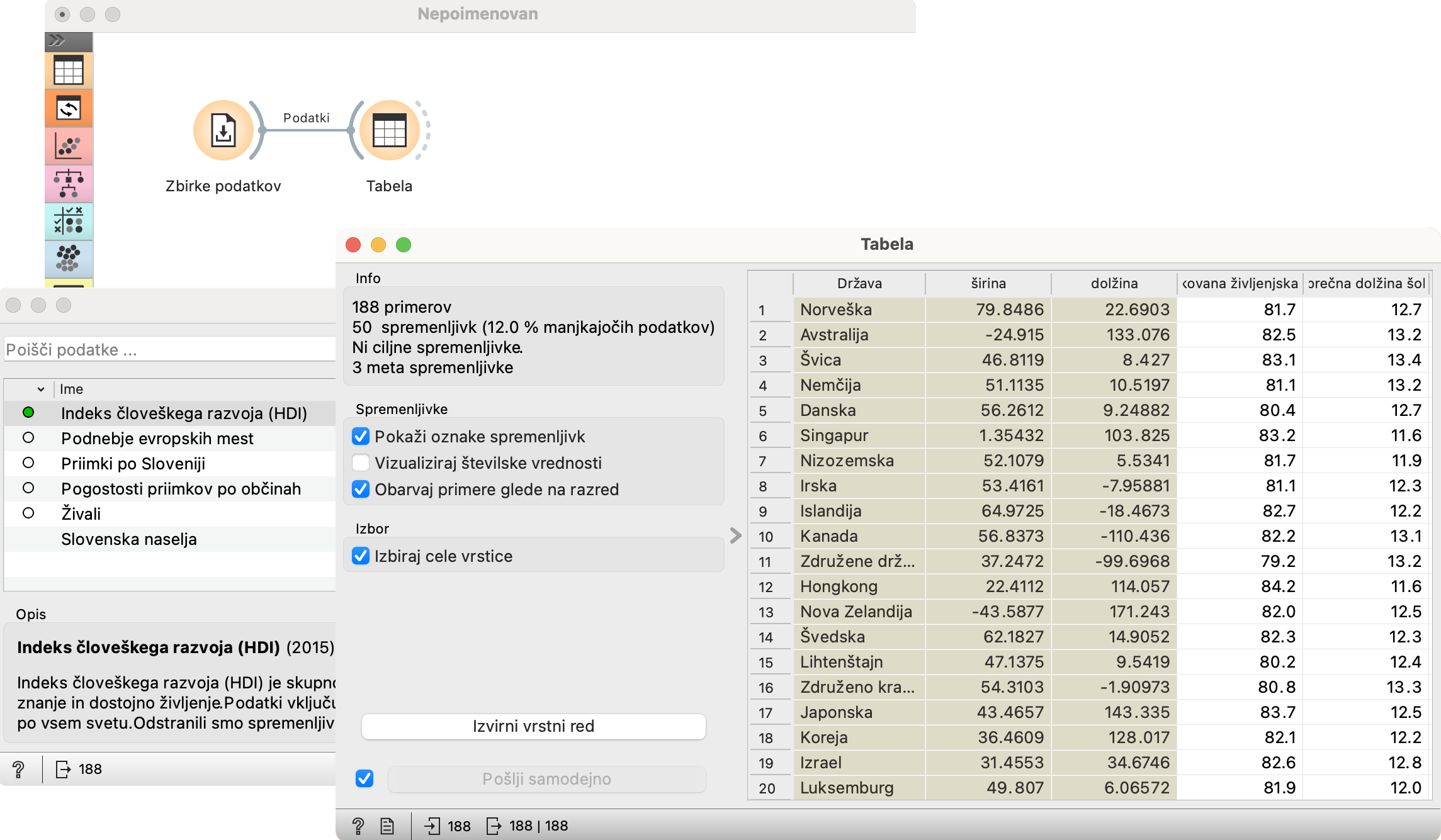
Zbirke podatkov zdaj daje podatke Tabeli. Karkoli prvi prebere, to drugi pokaže.
Poglavje 2: Igra tabel
... v katerem ugotovimo, da je celo s tako preprostim gradnikom, kot je Tabela, možno odkriti kaj zanimivega. Za konec pa vidimo še tipičen primer trika, kakršne izkušen uporabnik Oranga stresa kar iz obeh rokavov.
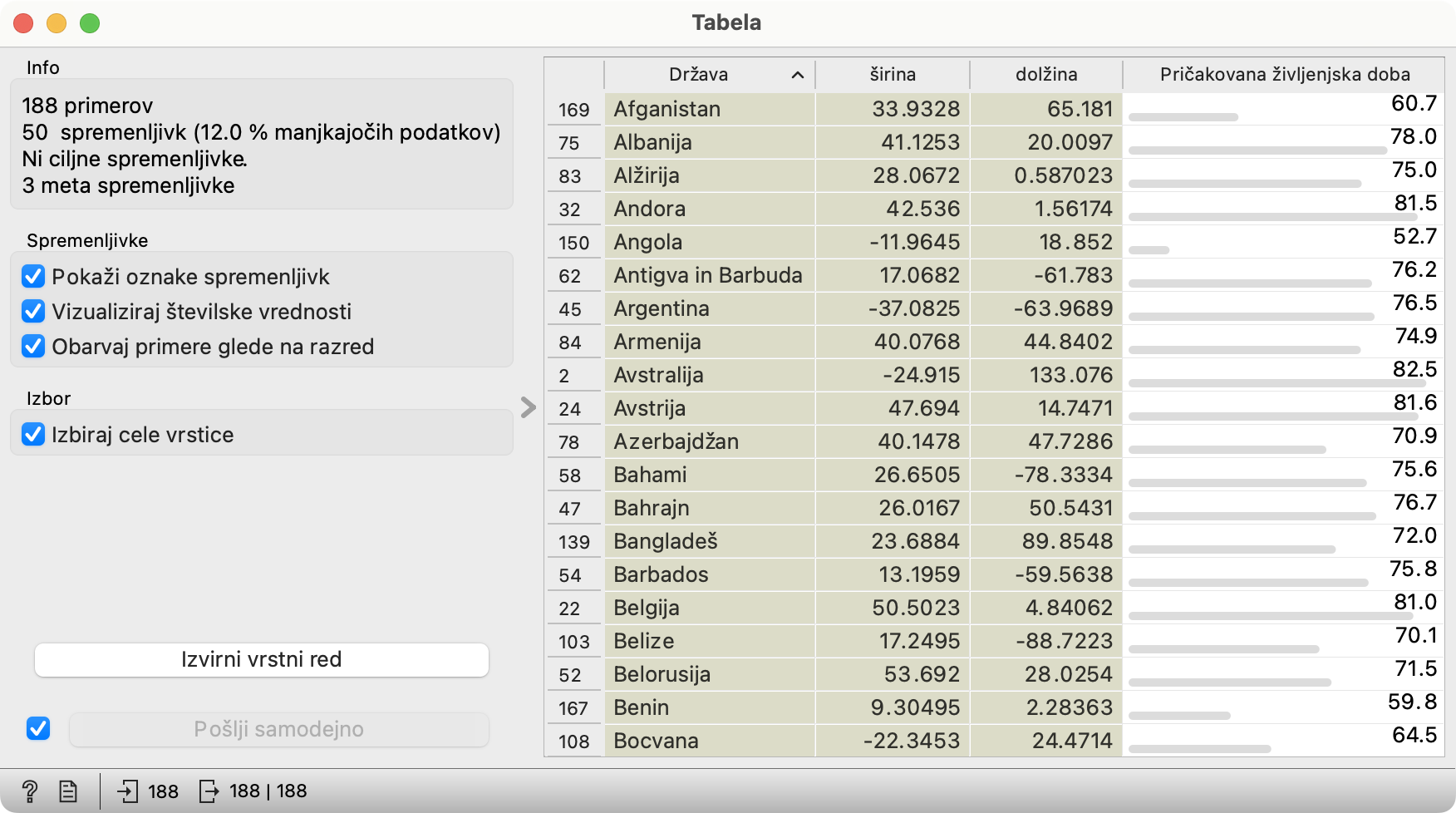
Ni potrebno biti posebej dober opazovalec, da vidimo, da gre za neke podatke o državah. Na levi strani gradnika preberemo, da jih je 188 in da so opisane s 50 spremenljivkami. Vidimo pa tudi, niso urejene ne po abecedi ne po kakem drugem očitnem kriteriju.
Orange ni Excel - urejanje po vrednostih v stolpcu je preprosto, le ime stolpca kliknemo. Če želimo urediti države po abecedi, kliknemo ime stolpca, Država. Če želimo padajoči vrstni red, kliknemo ponovno.
Mimogrede, številke na levi strani tabele kažejo zaporedno številko vrstice v vhodnih podatkih - tudi po tem, ko preuredimo tabelo. Afganistan, recimo, je bil na 169. mestu v vhodni tabeli. To zna biti kdaj priročno.
Poskusimo, ali razumemo.
Na vprašanja v priročniku lahko odgovarjate, dokler ne odgovorite pravilno. Po pravilnem odgovoru se splača prebrati razlago odgovora ali poti do njega. Ob nekaterih vprašanjih je ta na voljo že po prvem poskusu, čeprav napačnem, ob težjih pa že kar takoj.
V kateri državi na svetu živijo najdlje?
Čemu pa služi desna antena gradnika Tabela? Zna posredovati podatke naprej? Tabela kaže podatke, ne? Zakaj bi jih dajala? V večini gradnikov lahko izberemo (ali predelamo) podatke in ta izbor posredujemo naprej. V Tabeli lahko, na primer, izberemo pet najbolj dolgoživih držav in jih pošljemo v novo Tabelo.
Kam je šel levi del gradnika, ki vsebuje podatke o tabeli in nastavitve? Skrijemo in pokažemo ga s klikanjem na prostor med levim in desnim delom.
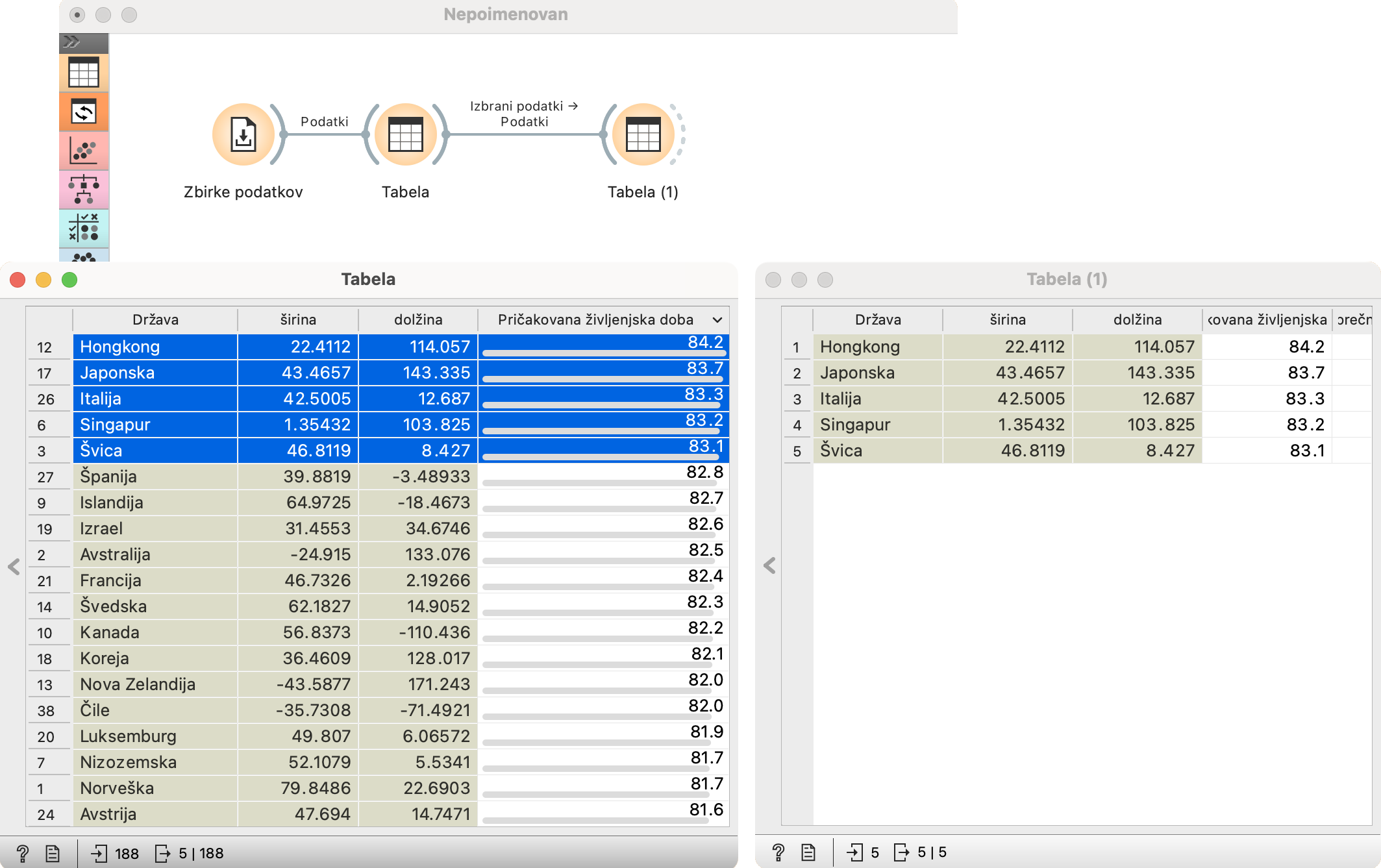
Le poskusite!
Kako preklicati izbor? Najpreprosteje tako, da kliknemo v prazno polje nad številkami vrstic, levo od imen stolpcev. Ob prvem kliku izbere celotno izbiro, ob naslednjem pa pobriše izbor.
Kaj pa, če ne izberemo ničesar? V tem primeru bo Tabela poslala naprej vse podatke.
Zdaj pa pride težko vprašanje.
Na katerem mestu je glede na dolžino življenja Slovenija?
Naloga ni bila nič posebnega, zanimiva pa je zato, ker kaže, da so Orangovi gradniki kot kocke Lego: meja je samo domišljija. Tale primer uporabe Tabele smo si v resnici izmislili pri pisanju tega priročnika. :)
Poglavje 3: Mami, jest nočem v šolo!
... ki nas nauči risati porazdelitve vrednosti v stolpcu, z vidika uporabe Oranga pa še enkrat - in lepše kot prej - pokaže idejo izbiranja podatkov v gradnikih.
Eden prvih stolpcev v tabeli pove, koliko let se v poprečju hodi v šolo v posamezni državi.
Kako se to obrne! Študenti so tako ukaželjni, da bi vlekli študij (in polni penzion v hotelu mama) do štiridesetega leta, ko bi le mogli.
Kot ve že vsak otrok (in predvsem otrok), je zaželeno v šoli preživeti čim manj let. V kateri državi bi se bilo potemtakem najboljše roditi? V kateri državi se hodi v šolo najmanj let? Odgovor znamo poiskati: uredimo države po stolpcu Povprečna dolžina šolanja. Sanjska država je … Burkina Faso.
Hm, morda ne. V letu in pol se človek komajda nauči brati, branje pa zna biti vendarle praktična veščina. Naslednji kandidat? Niger z 1,7. Mogoče tudi ne. Lahko vidimo celoten razpon, da se bomo lažje odločili?
Nazaj na platno. Gradnik, ki ga potrebujemo, se imenuje Porazdelitve. Mimogrede se bomo naučili še enega, učinkovitejšega načina dodajanja gradnikov: samo povlečemo povezavo iz Zbirke podatkov nekam v prazno in v menuju izberemo gradnik, ki ga želimo dodati na drugi konec povezave.
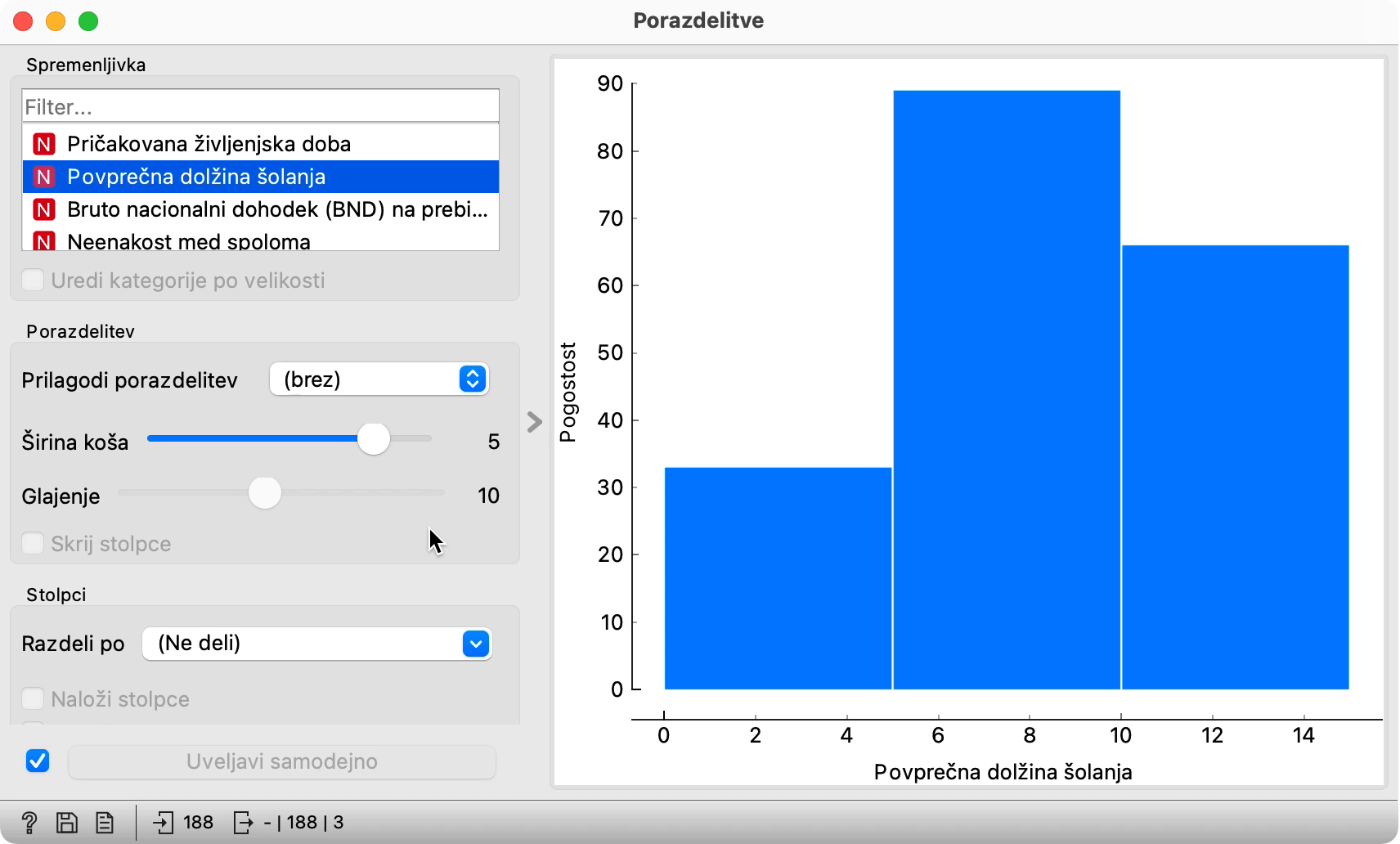
Gradnik (odpremo ga z dvoklikom nanj, kot običajno) nam pokaže porazdelitev vrednosti izbranega stolpca. Izberimo Povprečno dolžino šolanja. Dolžina šolanja je številska spremenljivka, pa še cela ni, saj gre za poprečje. Države zato razporedimo po koših: takšne, v katerih se šolajo do dve leti, takšne, kjer to počnejo 2-4 leta, pa 4-6 in tako naprej. Širino koša določimo z drsnikom.
(Zakaj ravno dve leti? Dve in pol zveni hecno, pet je preveč, pri enem letu pa ne dobimo več lepega, smiselnega razporeda, kar navadno pomeni, da imamo za tako natančno opazovanje premalo podatkov.)
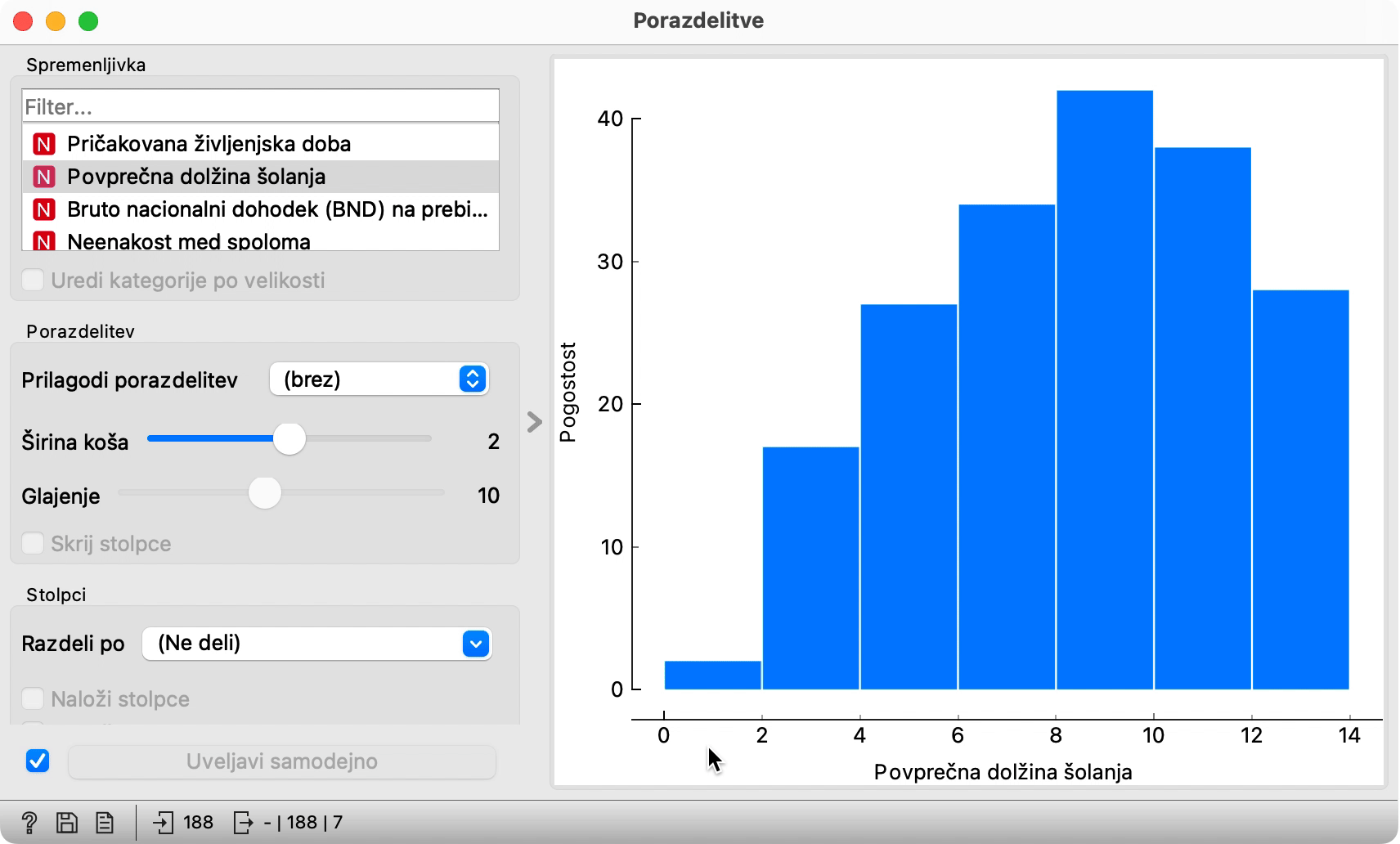
Malo se sprehodimo z miško po sliki. Če se ustavimo na enem od stolpcev, izvemo število in delež držav s takšno dolžino šolanja. Tako, na primer, vidimo, da obstajata le dve državi, v katerih otroci v povprečju trpijo (šolo) manj kot dve leti (vemo: Burkina Faso in Niger), in 17 takšnih, v katerih se šolajo med dvema in štirimi leti.
Bi radi izvedeli, za katere države gre? Preprosto, to že znamo. Iz gradnika Porazdelitve povlečemo povezavo v prazno, na njen konec dodamo Tabelo. Zdaj Porazdelitve dajejo podatke Tabeli. Podatki iz stolpca, ki ga izberemo, tako da kliknemo nanj (ali iz stolpcev, ki jih izberemo, tako da vlečemo čeznje ali klikamo tako, da hkrati držimo Ctrl ali Shift — saj znamo uporabljati računalnik), se pokažejo v Tabeli.
Poročilo s terena: nabor držav, v katerih se v povprečju šolajo 2-4 leta, smo ponudili dijakom ene mariborskih gimnazij, vendar so se jim skoraj soglasno odrekli. Skoraj pa zato, ker se je nekdo vseeno javil za Senegal. Zaradi nogometa, je rekel.
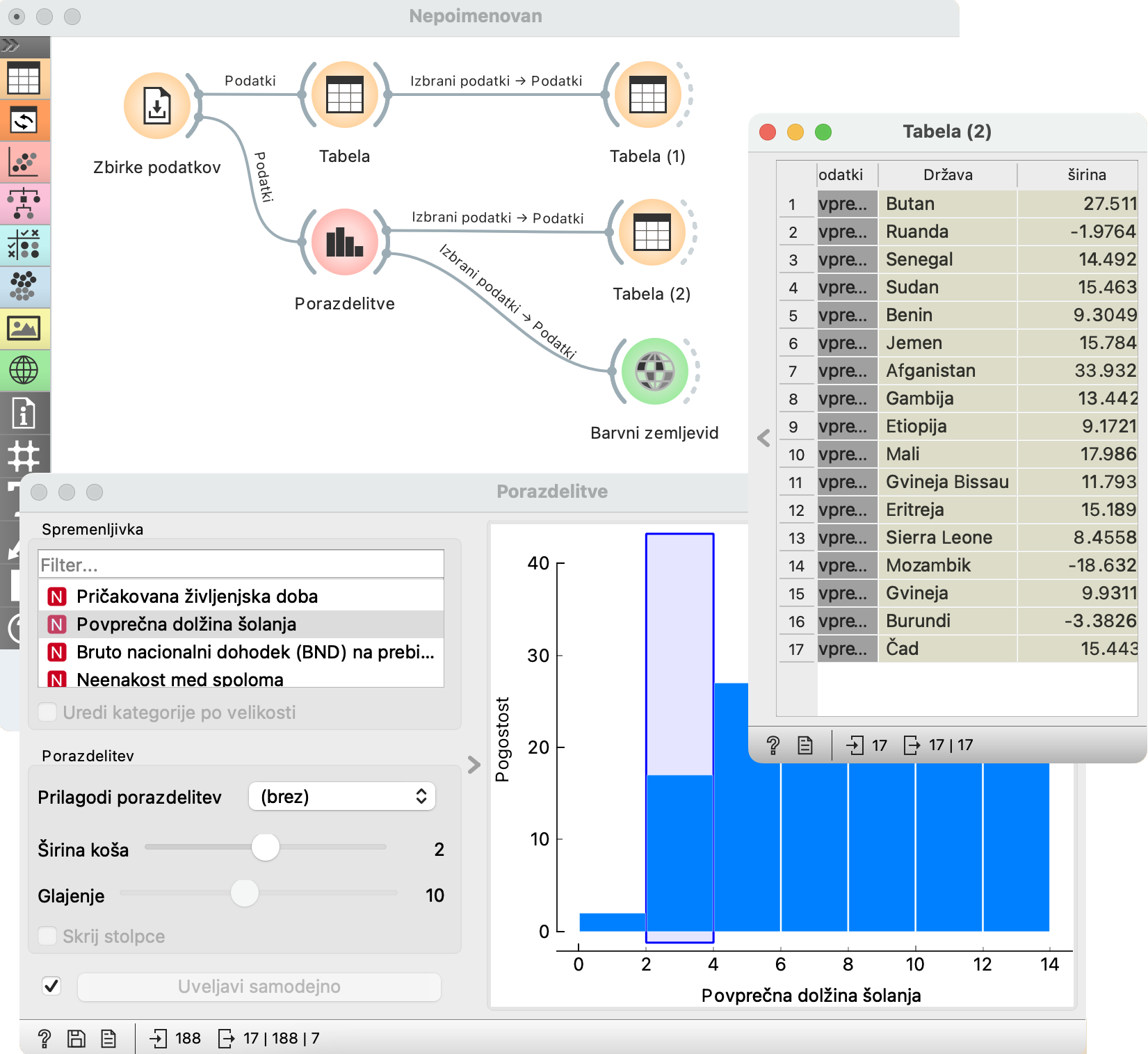
Sodeč po tabeli gre pretežno za afriške države. Zaupamo svojemu znanju zemljepisa ali pa bomo raje preverili? Je možno videti te države na zemljevidu?
Možno. A preden nadaljujemo, preverimo nekaj drugega. Namreč, ali še sledite.
Katera država izmed tistih v košu, v katerem se šolajo najdlje (12-14 let) ima najkrajšo pričakovano življenjsko dobo?
Preden zaključimo, pa še enkrat - in malo bolj abstraktno - pomislimo, kaj pravzaprav počne gradnik Porazdelitve. V njem izberemo neko spremenljivko. Gradnik razdeli njene vrednosti na intervale, »koše«, in prešteje, koliko držav (ali, v splošnem, vrstic) sodi v ta koš. Če je spremenljivka kategorična, kot, na primer, spol ali vzrok prometne nesreče, so »koši« seveda že določeni. Gradnik sicer zna še marsikaj: prek stolpcev lahko napne krivulje različnih oblik, jih deli glede na vrednost druge spremenljivke, računa verjetnosti... Samo v vednost.
Poglavje 4: Kje na svetu je Burkina Faso?!
... ki nas nauči postaviti podatke na zemljevid.
Za Orange obstajajo dodatki z novimi gradniki. Eden od njih je Geo, ki omogoča risanje zemljevidov. Namestimo ga, tako da ga izberemo v Nastavitve / Dodatki, potrdimo izbor in ponovno zaženemo Orange.
Orangeov dodatek zna risati dva zemljevida.
Običajni Zemljevid je zemljevid, v katerega so vrisane točke, ki ustrezajo primerom (vrsticam) iz tabele. Za to morajo vrstice seveda vsebovati podatek z zemljepisno lokacijo. Uporabimo ga lahko za risanje epicentrov potresov, prizorišč nogometnih prvenstev ali lokacij kakih drugih katastrof in opustošenj.
Barvnemu zemljevidu se v angleščini reče Choropleth map. Čudno besedo si bodo brez težav zapomnili vsi tisti med nami, ki znajo grško: χῶρος (koros) pomeni področje in πλῆθος (pletos) je večkratnost.
Tudi Barvni zemljevid zahteva tabelo, katere vrstice vsebujejo podatek o zemljepisni lokaciji, namesto da bi kazal točke, pa barva regije, ki jim te točke pripadajo. Regije lahko le označi, lahko pa jih pobarva glede na vrednost nekega drugega podatka iz te vrstice, na primer Povprečno dolžino šolanja. Če isti regiji pripada več vrstic, pa lahko regijo pobarva glede na to, koliko je teh točk ali pa glede na povprečno, največjo ali najmanjšo vrednost določenega podatka v teh vrsticah.
Risanje zemljevidov zahteva internetno povezavo, saj se zemljevidi nalagajo s spletnega strežnika.
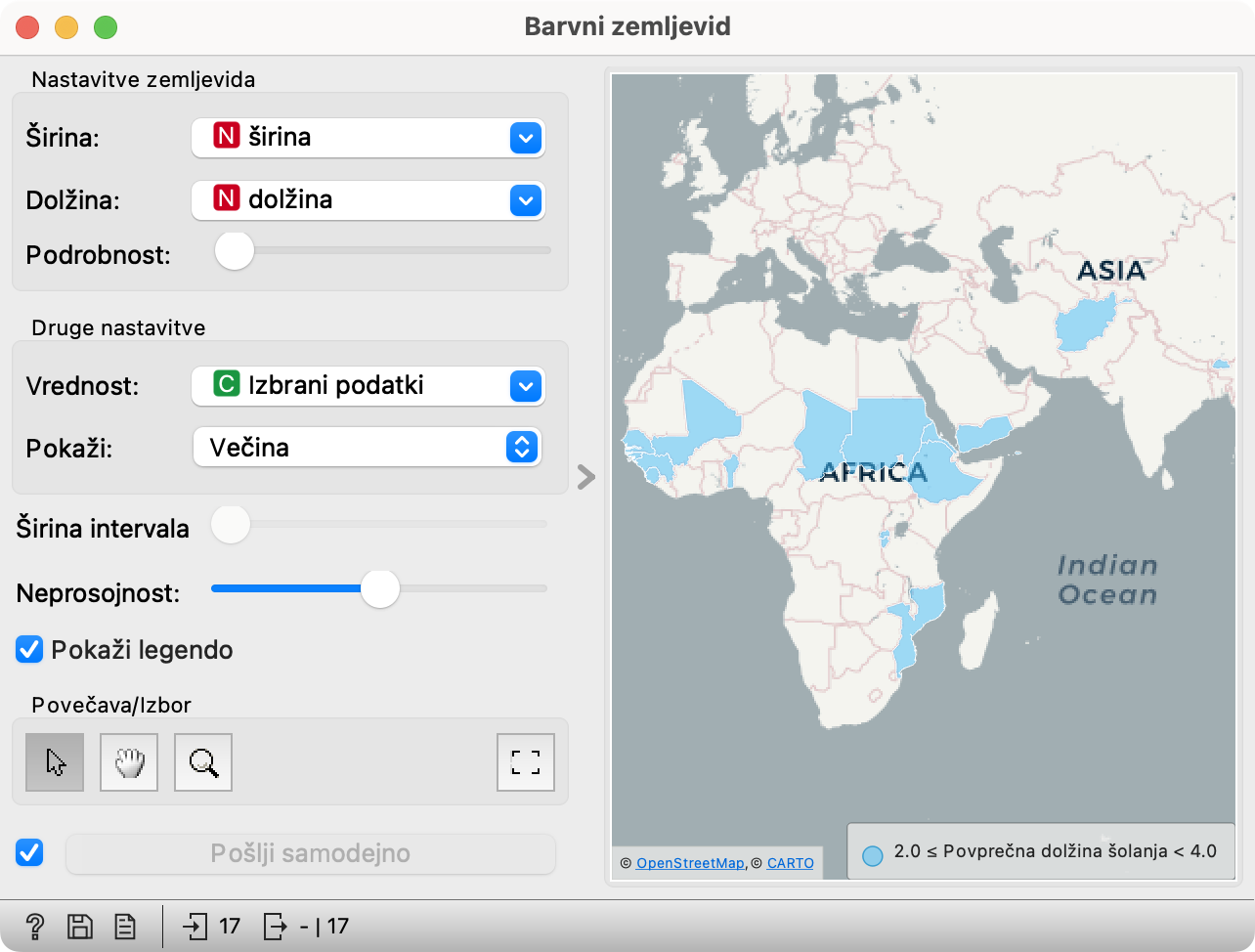
Ker raziskujemo države, bomo uporabili Barvni zemljevid. Priključimo ga na Porazdelitve in ga primerno nastavimo. Gradnik mora najprej vedeti, v katerih dveh stolpcih sta zapisani zemljepisni koordinati, na kateri se nanaša vrstica. Če najde stolpca, poimenovana širina in višina ali kaj podobnega v slovenščini ali angleščini, ju bo izbral kar sam. Sicer ju moramo nastaviti ročno.
Podatek v tabeli določa točko, barvni zemljevid pa kaže regije. Povedati mu moramo, kako velike regije želimo gledati - države, pokrajine, občine. To določimo z drsnikom Podrobnost, ki ga - v našem primeru, ko nas zanimajo države - povlečemo skrajno levo.
Zemljevid na sliki ne kaže imen držav. Če ga povečamo, jih pokaže in (delno) pokvari spodnjo nalogo.
Da, na zemljevidu vidimo, da so pobarvane večinoma afriške države in še tri druge. Ena se skoraj drži Afrike, vendar jo težko poimenujemo, če ne znamo dovolj zemljepisa. Druga je verjetno Afganistan. Tretje pa skoraj že ne vidimo, saj je tako manjhna. Izvedimo, za katere države gre!
Katera je torej mala azijska država, v kateri ne hodijo prav dolgo v šolo?
Tako kot smo se v prejšnjem poglavju naučili le osnovne rabe gradnika Porazdelitve, smo tudi le povohali Barvni zemljevid. Za zdaj ga znamo uporabiti za to, da pokaže izbrane regije. V prihodnjem poglavju bomo znali obarvati regije z različnimi barvami. V resnici je z njim možno početi še veliko več, a ne na teh podatkih.
Poglavje 5: Bolj ali manj modre države
... ko nas gradniki presenetijo z več izhodi, zato se naučimo izbirati med njimi.

"... kliknemo ikonico v spodnji vrstici gradnika, tisto, zraven katere je številka 3" smo napisali v razlagi rešitve vprašanja iz prejšnjega poglavju. Številka 3 seveda pove velikost izhodne tabele, tri države. Tam pa je pravzaprav še ena številka, 17. In ko kliknemo ikonico, da dobimo predogled - ali pa tudi le postojimo z miško na njej - vidimo, da nima le ene izhodne table, temveč dve.

Še pestrejši je izhod Porazdelitev: ta daje kar tri tabele.
Tri izhodne tabele, antena pa le ena sama. Kako se odločamo - pravzaprav, kdo se odloča - katero tabelo bo dobil Barvni zemljevid, ki je priključen na Porazdelitve?
Odloča, seveda, Orange. Mi pa ga lahko preglasujemo. Prva izhodna tabela, Izbrani podatki, je le privzeta. Če bi raje opazovali katero drugo, dvokliknemo povezavo.
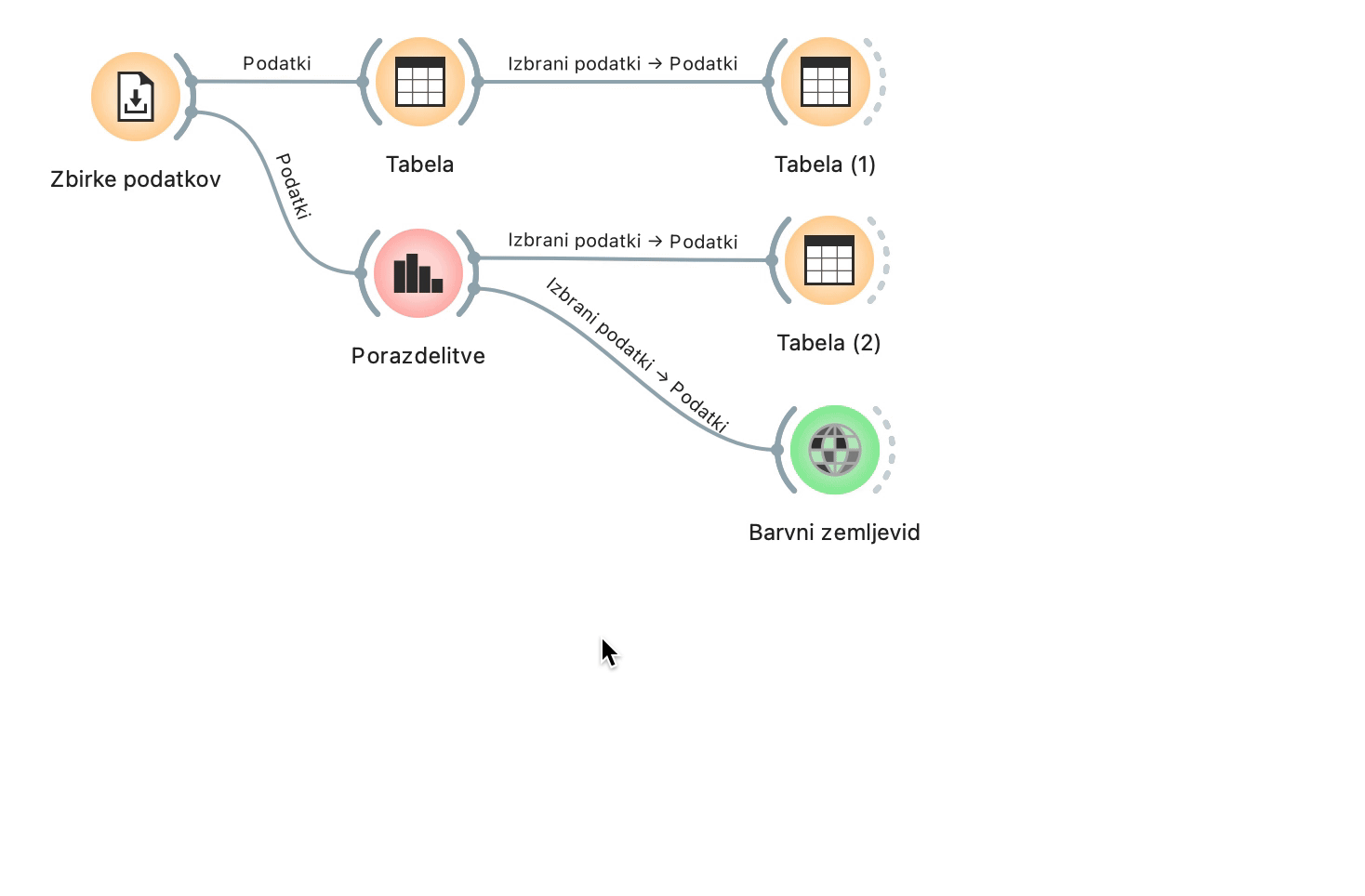
Statusna vrstica gradnika Porazdelitve nam razodeva, da je dobil tabelo s 188 vrsticami in daje tri tabele, ki imajo po 17, 188 in 7 vrstic:
![]()
Prva, tista s 17 vrsticami, vsebuje izbrane države - če je izbran drugi stolpec. Če kateri drugi, ali več drugih, ali nobeden, bo številka seveda drugačna.
Druga tabela ima 188 vrstic. Vsebuje torej vse podatke, a z dvema novima stolpcema. Kako se imenujeta, lahko vidimo v predogledu ali v novi tabeli, še bolj koristno pa bo, če ju poiščemo v Barvnem zemljevidu, v spustnem seznamu, s katerim izbiramo Vrednost. (Seveda po tem, ko smo v Barvni zemljevid pripeljali to tabelo namesto prve.)
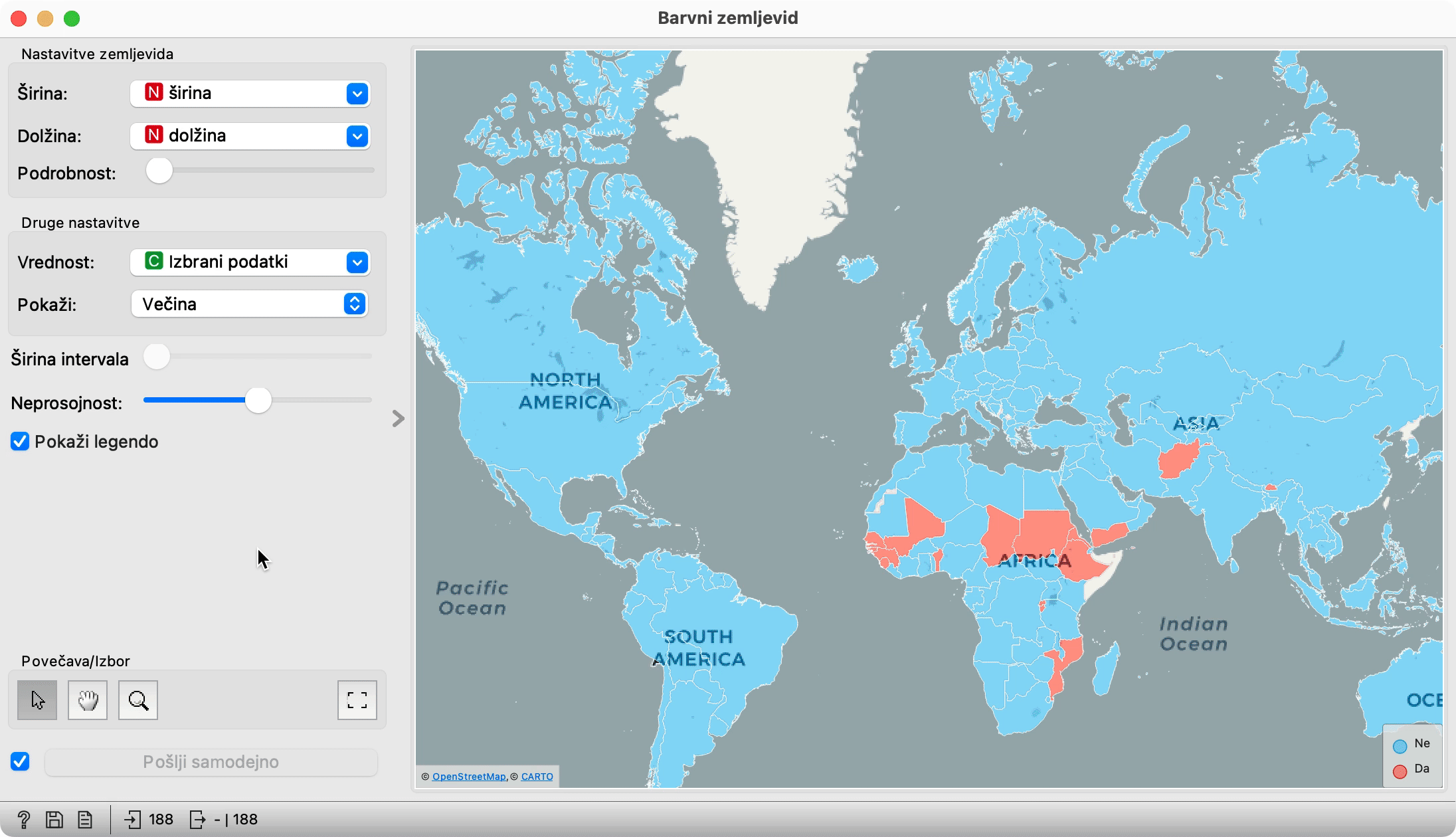
Stolpec Izbrani podatki pove, ali je posamična država izbrana ali ne. Zemljevid bo obarval vseh 188 držav, barvo pa izbiral glede na to, ali je država med izbranimi ali ne.
Stolpec Koš pa je ime koša. Države so pobarvane glede na to, v katerem košu se nahajajo. Od modrih, kjer se šolajo najmanj, pa prek rdečih, kjer se malo dlje, in potem prek drugih barv do rožnatih, kjer se skoraj najdalj in modrih, kjer se najmanj.
Ljudje naj bi razlikovali med 10 milijoni različnih barv. Praktične izkušnje kažejo, da jih od tega moški prepoznajo 5-6, ženske pa ostalih 9999995. Znanost pritrjuje: ženske so v razlikovanju barv dokazano boljše od moških (p<0.001).
Dragi bralec! Če ste moškega spola, se vrnite v Porazdelitve in povečajte širino koša na 5. (Če ste ženska, storite enako. Tako boste videli svet skozi moške oči in nas naslednjič v trgovini z oblekami lažje razumele. Hvala.)
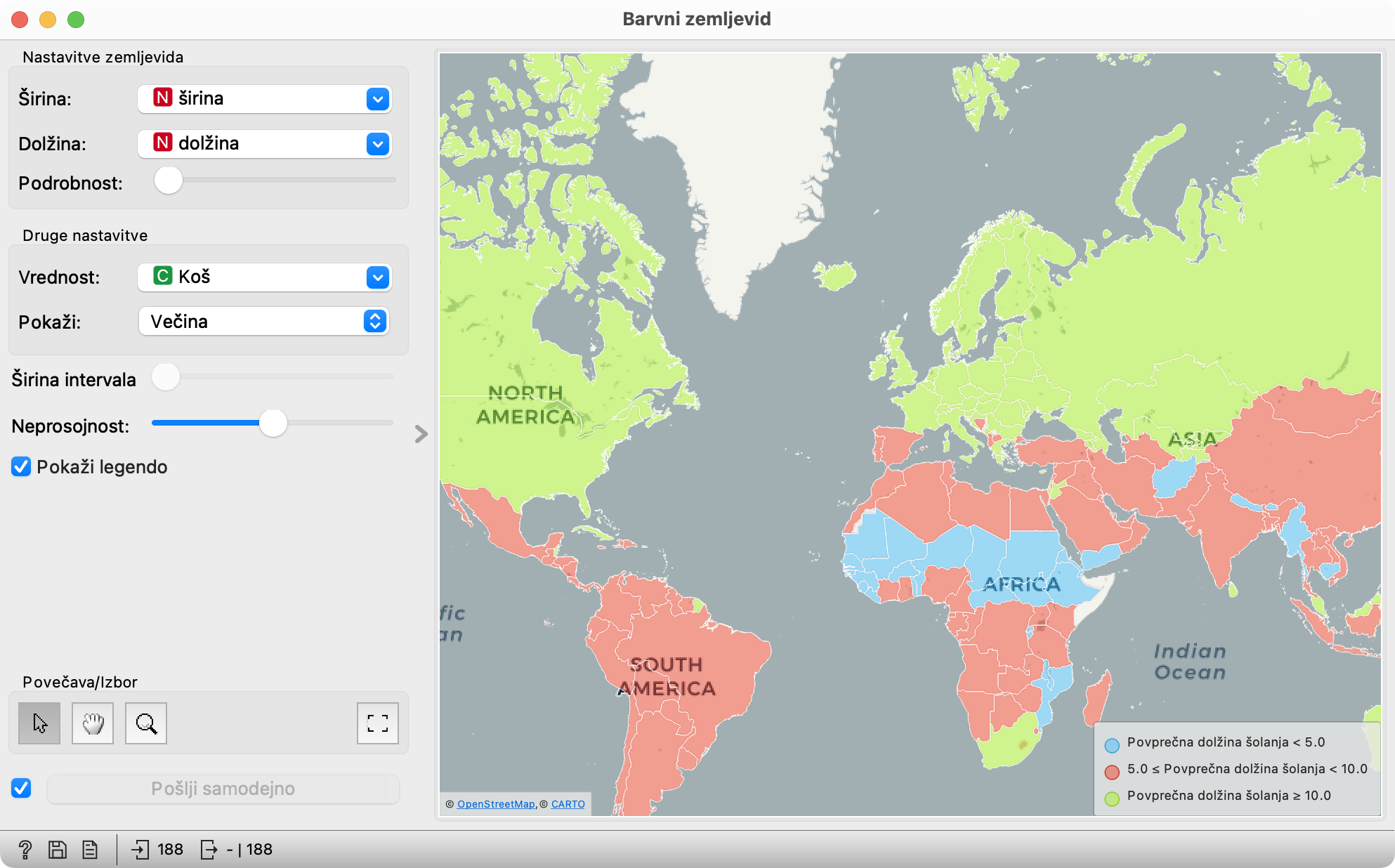
Toliko o drugi tabeli. Pa tretja? Pomen te pa odkrijte sami. (Nasvet: ne pošljite je v Barvni zemljevid temveč v Tabelo. Spremenite širino koša nazaj na, recimo, 2.)
Tretja tabela, Podatki o porazdelitvi, vsebuje dva stolpca. Če vemo, kaj pomenita, lahko brez seštevanja odgovorimo na vprašanje, kakšna je vsota vrednosti v drugem. Kakšna?
Večina gradnikov ima več izhodov. Praktično vsi, v katerih lahko izberemo podmnožico podatkov, imajo vsaj dva: enega, na katerega gradnik pošlje le izbrane podatke, in drugega, na katerem dobimo vse podatke in dodatni stolpec, ki pove, kateri od njih so izbrani. To se morda zdi odveč, v resnici pa se bo izkazalo za praktično. Videli smo tudi, da Orange izbere nek privzeti izhod (izjema so gradniki, kjer ni očitno, kateri izhod naj bi bil privzet). Če nam izbor ni všeč, ga pač spremenimo.
Poglavje 6: Pametni živijo dlje
... z novim gradnikom, ki nam bo pomagal raziskovati povezave med pari stolpcev.
Malo smo zakomplicirali. Torej odkomplicirajmo. Pobrišimo vse, razen Zbirke podatkov: izberemo vse gradnike in pritisnemo Del ali Backspace.
Podatke zdaj pošljimo naravnost v Barvni zemljevid.
Če kot Vrednost izberemo Povprečna dolžina šolanja, bomo videli podobno sliko kot prej. Širino koša določamo z drsnikom Širina intervala.
Namesto povprečne dolžine šolanja lahko izberemo tudi kaj drugega, recimo življenjsko dobo. In vidimo, da je slika podobna: kdor je dolgo v šoli, je tudi dlje na svetu.
Moremo to preveriti bolj neposredno? Ne tako, da v Barvnem zemljevidu izmenjujemo dve vrednosti in po spominu primerjamo sliki? Prav gotovo. Ko bi ne bilo tako, najbrž ne bi vprašal, ne?
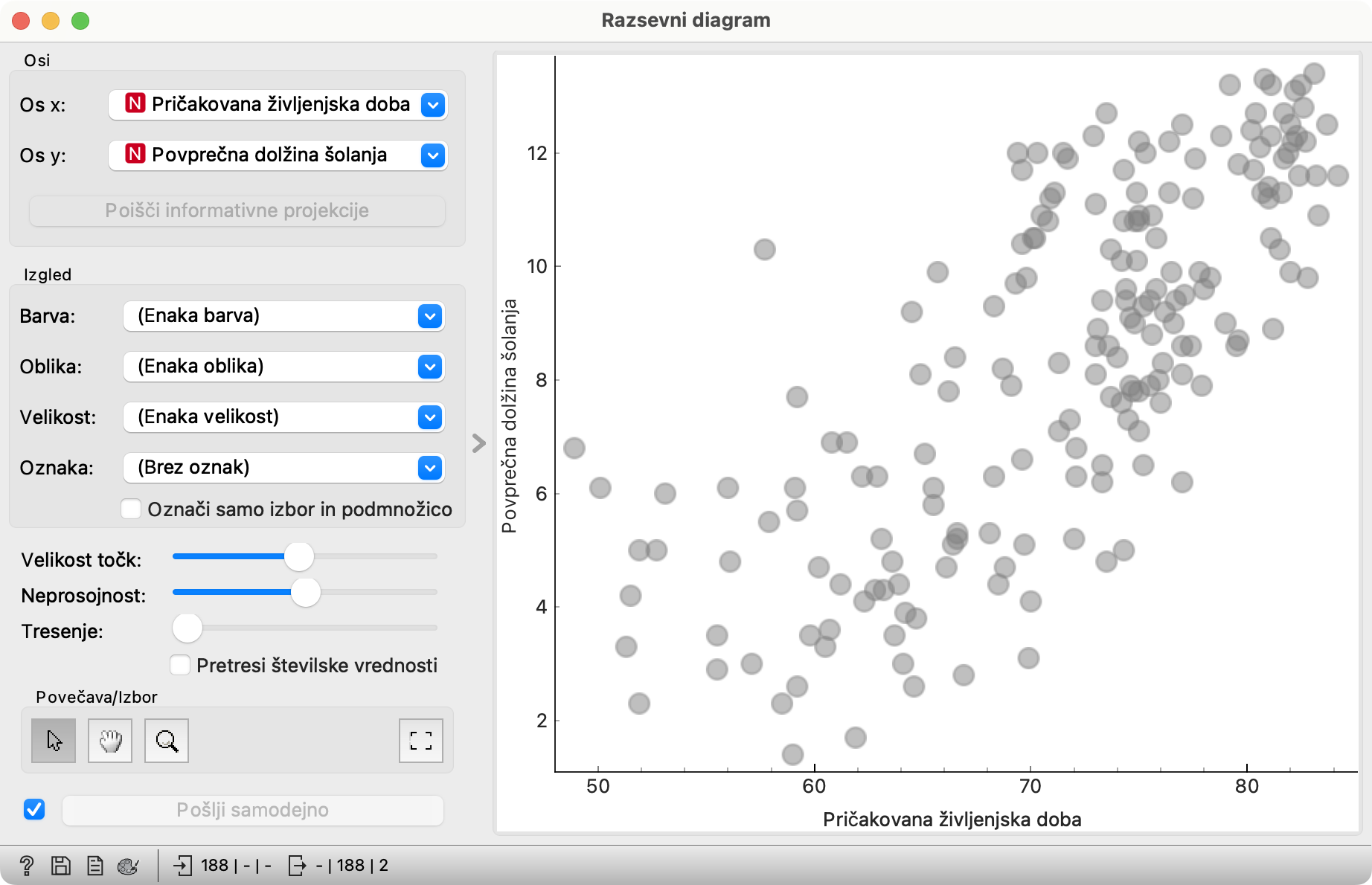
Na Zbirke podatkov priključimo Razsevni diagram. Ta je namenjen opazovanju povezave med dvema stolpcema (ali še kakim zraven).
Za razliko od Porazdelitev in Barvnega zemljevida Razsevni diagram ne združuje podatkov. Tu ni košev: vsaka vrstica (torej država) ustreza eni točki diagrama. Njene koordinate so določene z vrednostima dveh spremenljivk. Orange vzame kar prvi dve, v našem primeru Pričakovano življenjsko dobo in Povprečno dolžino šolanja. To je že skoraj to, kar hočemo, vendar ju raje zamenjajmo, tako da bo os x kazala čas šolanja in os y čas življenja.
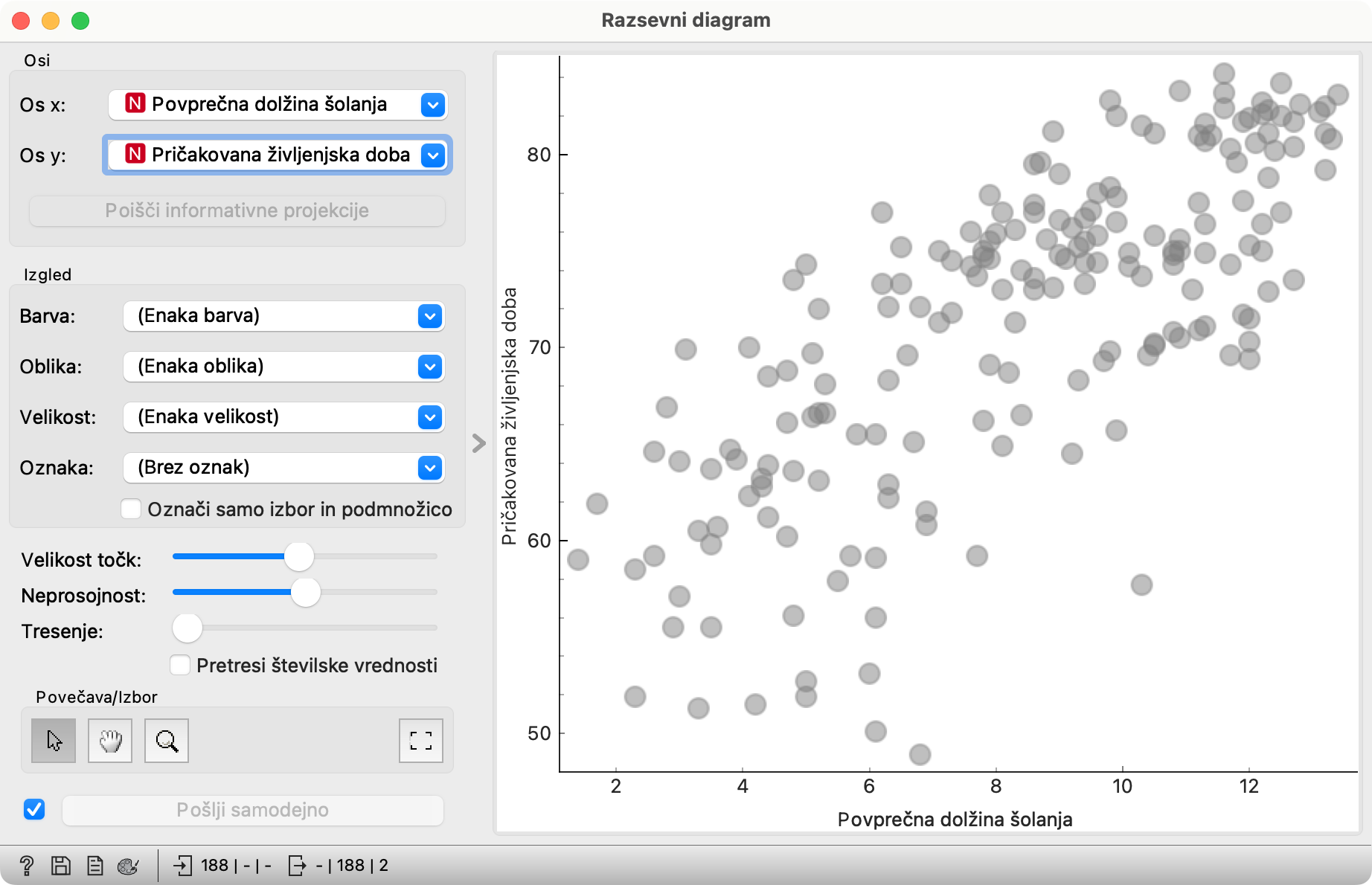
Zakaj je to potrebno? Zato, ker smo iz šole vajeni brati grafe tako, kot da je x neodvisna in y odvisna spremenljivka.
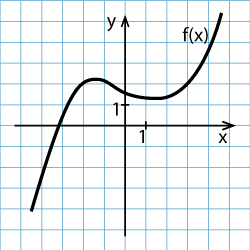
Opravičujem se vsem, ki jih je gornje prestrašilo; bom povedal lepše. Pa še narisal bom. Pri matematiki smo morali - popravite me, če vam morda ni bilo treba - na neizbežni karirasti papir risati grafe funkcij. Imeli smo neko funkcijo y = f(x) in graf je povedal, kakšna je vrednost y pri določenem x. Češ, ti si izmisli x, pa ti povem, kakšen bo pripadajoči y. Ko je na tule naslikani funkciji x enak 3, je f(x) (torej y) enak 2. Statistiki bi radi zveneli še bolj učeno kot matematiki, zato x-u rečejo neodvisna spremenljivka (saj si ga lahko izmislimo), y-u pa odvisna (saj je njegova vrednost odvisna od x-a).
Tule namigujemo že na vzročno povezavo. Morda je ni. Lahko je tudi obratna: morda je dolgoživejšim ljudem manj škoda časa za šolo. Ali pa imata spremenljivki skupen vzrok. Vzročnost je navadno težko pokazati zgolj iz podatkov in diagramov.
No, zaradi tega drila smo vajeni enako brati vse tovrstne grafe. Če se ozremo nazaj na razsevni diagram - namreč drugi, spodnji - vidimo dolžino šolanja kot neodvisno spremenljivko, dolžino življenja pa kot odvisno (od dolžine šolanja). Kar je morda to, kar smo hoteli raziskati: kako dolžina šolanja vpliva na dolžino življenja: je res, da ljudje v državah, v kateri se šolajo dlje, tudi dlje živijo? Povej mi, koliko časa hodijo v šole, pa ti povem, koliko časa živijo.
Razsevni diagram vsekakor kaže takšen trend. Če pokljukamo še Pokaži mrežo in Pokaži regresijsko premico, bomo lahko trend celo uštevilčili: regresijska premica se na intervalu od dveh let in pol do dvanajstih let in pol šolanja vzpne od 60 do 80 let življenja. Kdor se šola 10 let dlje, si podaljša življenje za 20 let. Dodatno leto šole prinese dve dodatni leti življenja. Plačaš eno, dobiš dve.
Dijake smo vprašali, če so pripravljeni sprejeti takšen dogovor: za vsako leto več v šoli boš dve leti dlje živel. Zviteži so vprašali, kdaj bo treba hoditi v šolo in pojasnili smo drobni tisk: v šolo hodiš, ko si mlad, dlje boš živel, ko boš sedemdeset. In prejeli odgovor: »No deal."
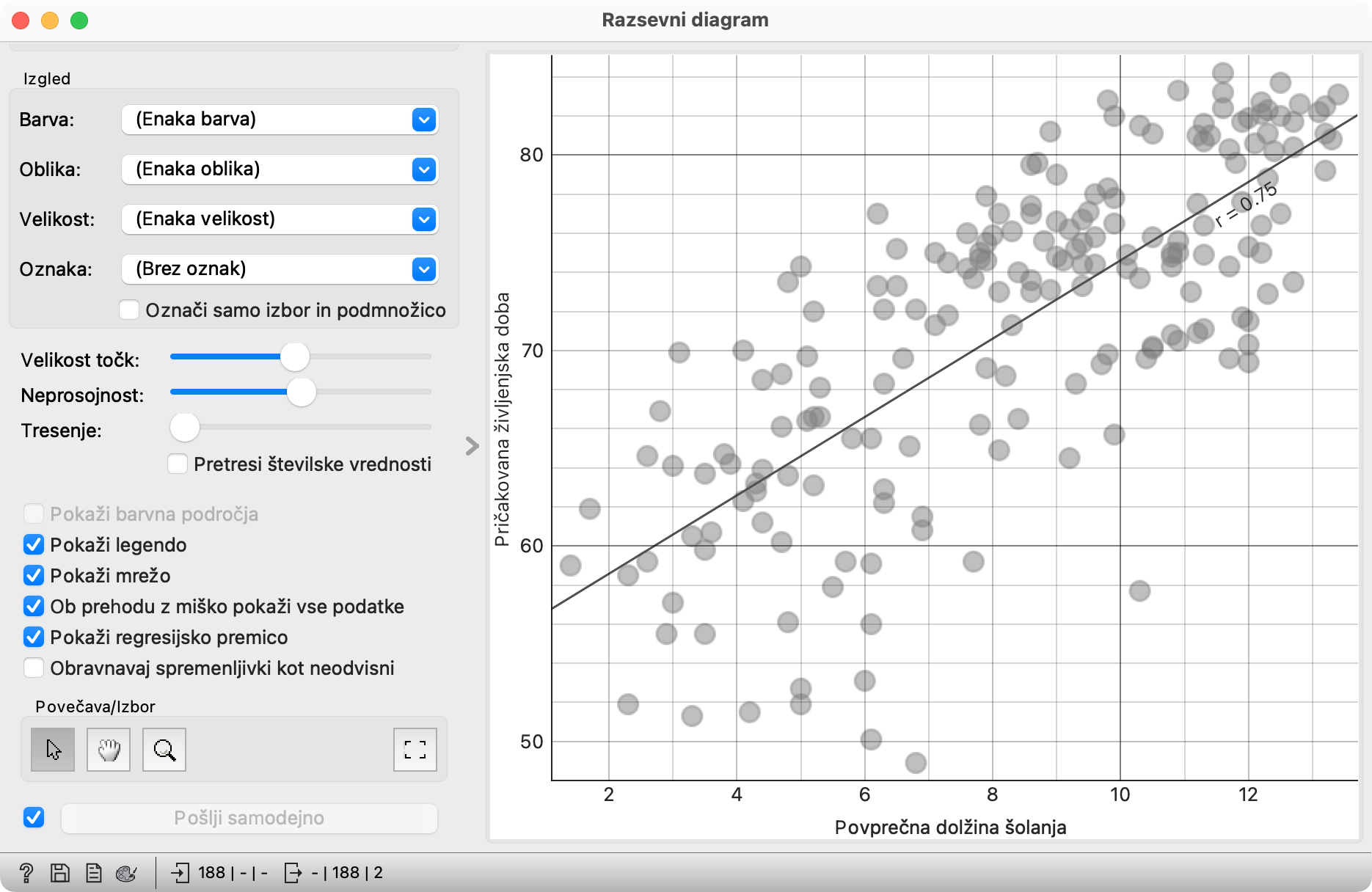
Tule je potrebno biti previden, zelo previden. Pozorni moramo biti na to, o čem govorijo podatki: ne o ljudeh temveč o državah. Daljše življenje uživa družba in je rezultat načina življenja družbe, vključno z njeno (splošno) izobraženostjo. Posameznik uživa prednosti družbe, v kateri živi, ne da bi nujno sam prispeval k njej.
In, seveda, povezava ni nujno vzročna. Možno, zelo možno je, da ljudje v državah z boljši izobraževalnim sistemom tudi boljše in dlje živijo, oboje pa je istočasna posledica nečesa čisto tretjega.
Razsevni diagram, preprosto, pokaže morebitno povezavo med dvema spremenljivkama. Povezava je lahko linearna, torej sledi neki ravni črti, ali bolj zavijajoča. Prav tako je lahko tesna, ali pa malo ohlapnejša. Razsevni diagram tudi dobro pokaže primere, ki od trenda odstopajo. Vidimo na sliki kaj takšnega?
Poglavje 7: Kdo je nasrkal?
... ki nas ponovno pouči, kako koristno je, da gradniki omogočajo izbiranje podatkov.
Nekdo da je nasrkal?
Da. Nekje hodijo v šole dobrih deset let (v poprečju), potem pa umrejo pri manj kot šestdesetih (v poprečju). Namreč tista točka desno spodaj. Nasrkali so vsi, ki so pod črto, ampak tile reveži pa še posebej. Kdo je to?
Razsevni diagram ima še precej nastavitev. Točke so lahko različnih barv, oblik in velikosti; barvamo, oblikujemo in veličamo(?) jih lahko glede na vrednosti spremenljivk. Velikost, recimo, bi lahko ustrezala bruto družbenemu proizvodu. Poleg tega pa lahko točke označimo (angl. label). Pa dajmo: za Velikost izberimo Bruto nacionalni dohodek (nekaj podobnega kot BDP), kot oznako pa Država. Ko smo to storili, dobimo eno samo veliko neberljivo gnezdo oznak, zato obkljukajmo še Označi samo izbor in podmnožico. Potem označimo tiste reveže desno spodaj (tako da potegnemo čeznje z miško) in izvemo za koga gre: Južna Afrika (uradno Republika Južna Afrika).
Te špekulacije samo s temi podatki ne moremo potrditi ali ovreči. Kakšne podatke pa bi potrebovali? (Odgovor: podatke, razdeljene glede na raso. Ali kar primeren vzorec podatkov posameznikov.)
Zakaj ravno Južna Afrika? Pošpekulirajmo: morda gre za državo z velikimi socialnimi razlikami. Morda se premožnejši (kar najbrž še vedno pomeni: belci) dolgo šolajo, revnejši (najbrž večinoma črnci) pa mladi umirajo. In v neizprosni igri statistike in številk jih to postavi globoko pod črto.
Precej visoko je ogromna točka. Prebivalci te države veliko zaslužijo, se ne pretegnejo v šoli in še dolgo živijo. Katera država je to?
Morda se vseeno ne bi selili tja. Države čisto desno zgoraj so videti povsem privlačno. Kdo so? Označimo jih, pa bomo videli.
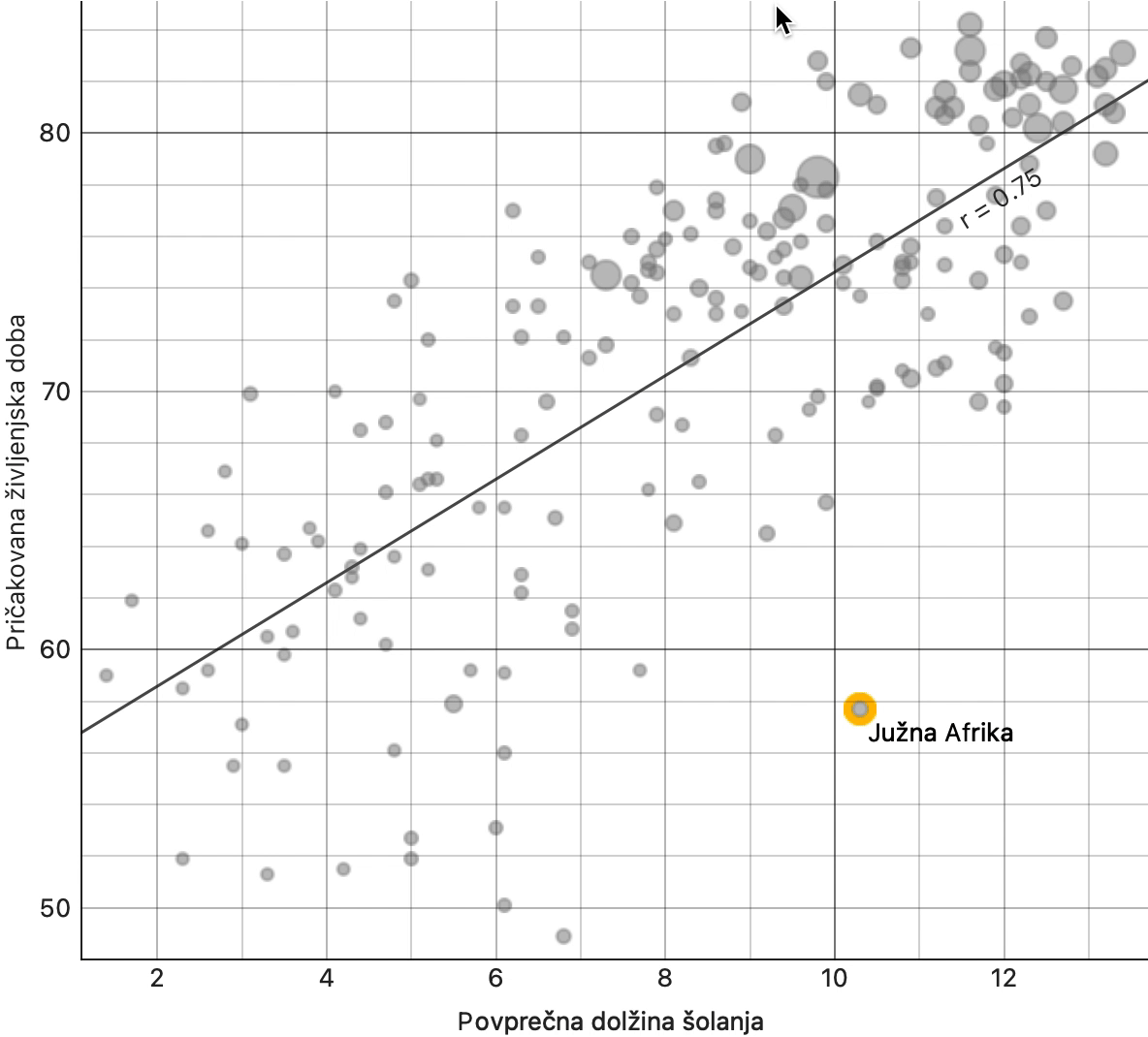
Pravzaprav ne bomo videli. Vsi bi radi bili tam, pa so se malo nagnetli in njihova imena so napisana eno čez drugo.
Tudi Razsevni diagram ima izhode. Za začetek ga lahko priključimo na Tabelo in dobimo seznam izbranih držav in vseh njihovih lastnosti. Pretežno po pričakovanjih Evropa, severna Amerika, Japonska in Avstralija, kot zanimivost pa še Čile in … Kuba! Še lepše bo, če Razsevni diagram priključimo na Barvni zemljevid. Če ga že ravno imamo in poznamo.
Zdaj točno vidimo, za katere dele sveta gre.
Poglavje 8: Vsaka riba ni slanik
... ko se pokaže, da imajo gradniki lahko tudi več vhodov. Kar je imenitno.
Zdaj torej vemo, kdo so srečneži iz razsevnega diagrama. Zgoraj desno so Evropejci (in še nekaj drugih). Moremo to obrniti? Evropejci so desno zgoraj?
Ne nujno. Kot je - na lastno škodo - ugotovil že kapitan Vrungel, je resda vsak slanik riba, ni pa zato ravno čisto vsaka riba slanik. Tako kot obstajajo ribe, ki niso slaniki, morda obstajajo tudi evropske države, ki niso zgoraj desno.
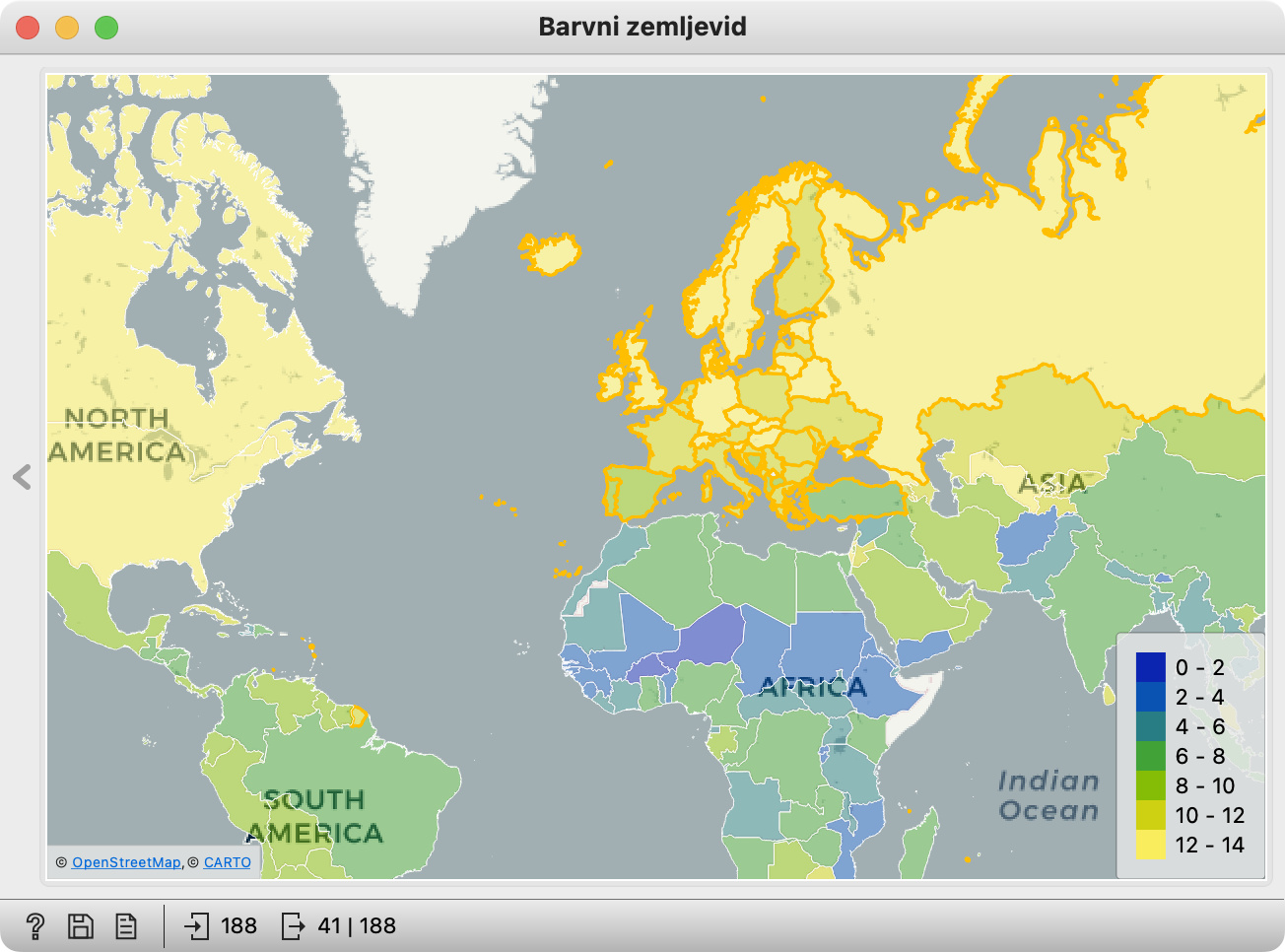
Da ugotovimo, kako je s tem, moramo izbrati evropske države in videti, kje jih najdemo v razsevnem diagramu. Odpremo torej zemljevid in izberemo evropske države. Vsaj tako, približno. Kliknemo nekje nad Islandijo in povlečemo pravokotnik tam nekam v Turčijo. Izbrane države bodo označene in gradnik bo, kot vidimo v statusni vrstici, dal na izhod dve tabeli: podatke o izbranih državah (v primeru na sliki jih je 41, pri vas je lahko kakšna manj ali več) in podatke o vseh državah.
Zdaj pa je potrebno ta izbor prenesti v Razsevni diagram. Vendar ne tako, da bo ta kazal samo izbrane države. Še vedno mora kazati vse države iz Zbirke podatkov, te, ki smo jih označili na Barvnem zemljevidu, pa mora označiti.
Način, na katerega to naredimo, je preprost in intuitiven. Preprosto povežemo Barvni zemljevid z Razsevni diagram. Prej lahko še malo odmaknemo Razsevni diagram in kompanijo, ki mu sledi - toliko, zaradi preglednosti.
Odprimo Razsevni diagram. Če imate v njem še vedno označene gornje desne točke, kliknite nekam v prazno, da odstranite izbor, saj nam zdaj le kvari sliko. Sicer pa naj bo gradnik nastavljen tako kot prej: Oznaka naj bo še vedno Država, in Označi samo izbor in podmnožico naj bo obkljukan. Izbor je tisto, kar izberemo v gradniku, podmnožica pa tisto, kar je gradnik prejel na dodatnem vhodu.
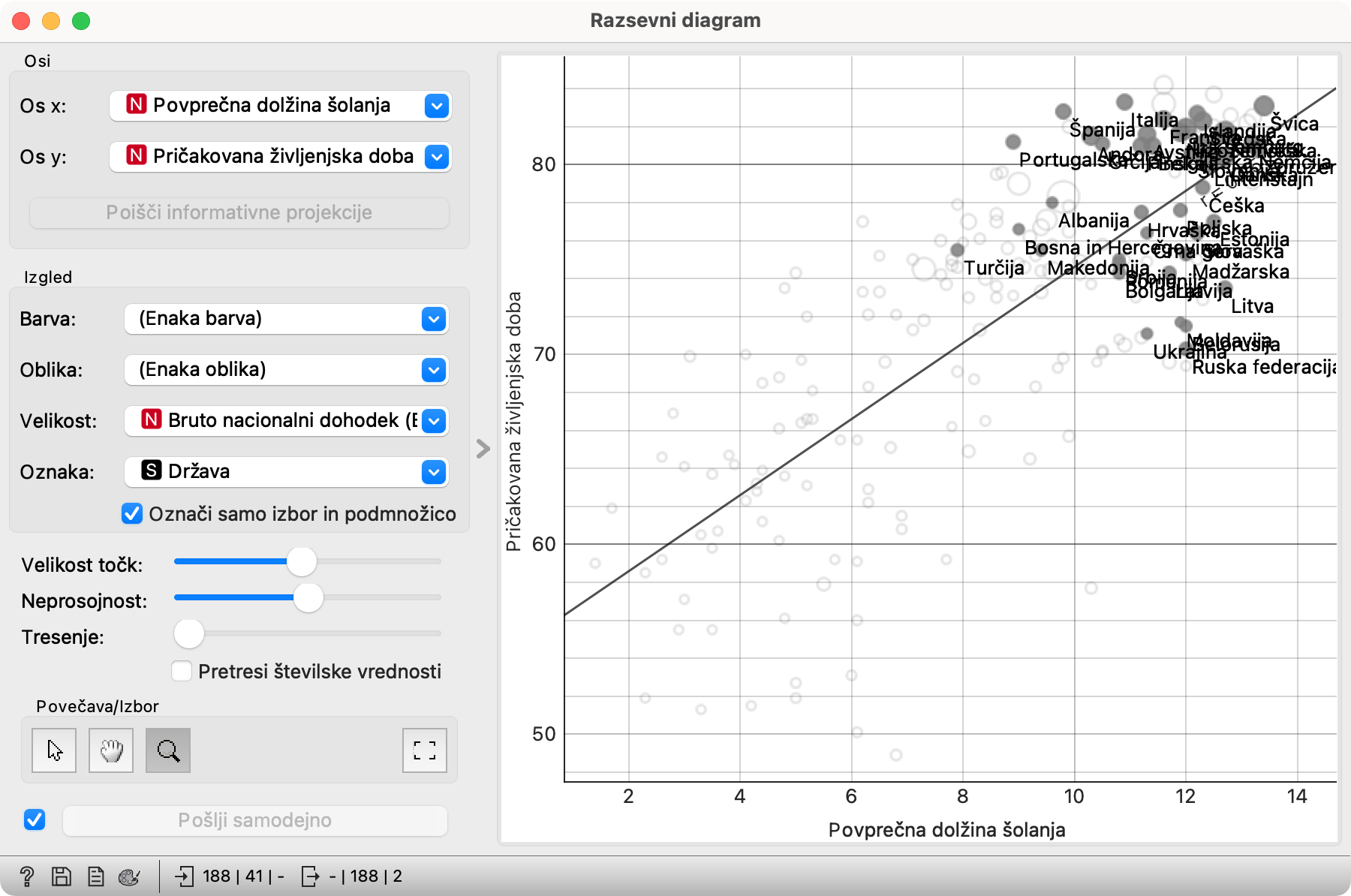
Zdaj vemo: Evropa je desno zgoraj. Ne samo Evropa, vendar vsa Evropa.
Mimogrede, če bi radi videli imena držav, lahko povečate zgornji desni del diagrama.
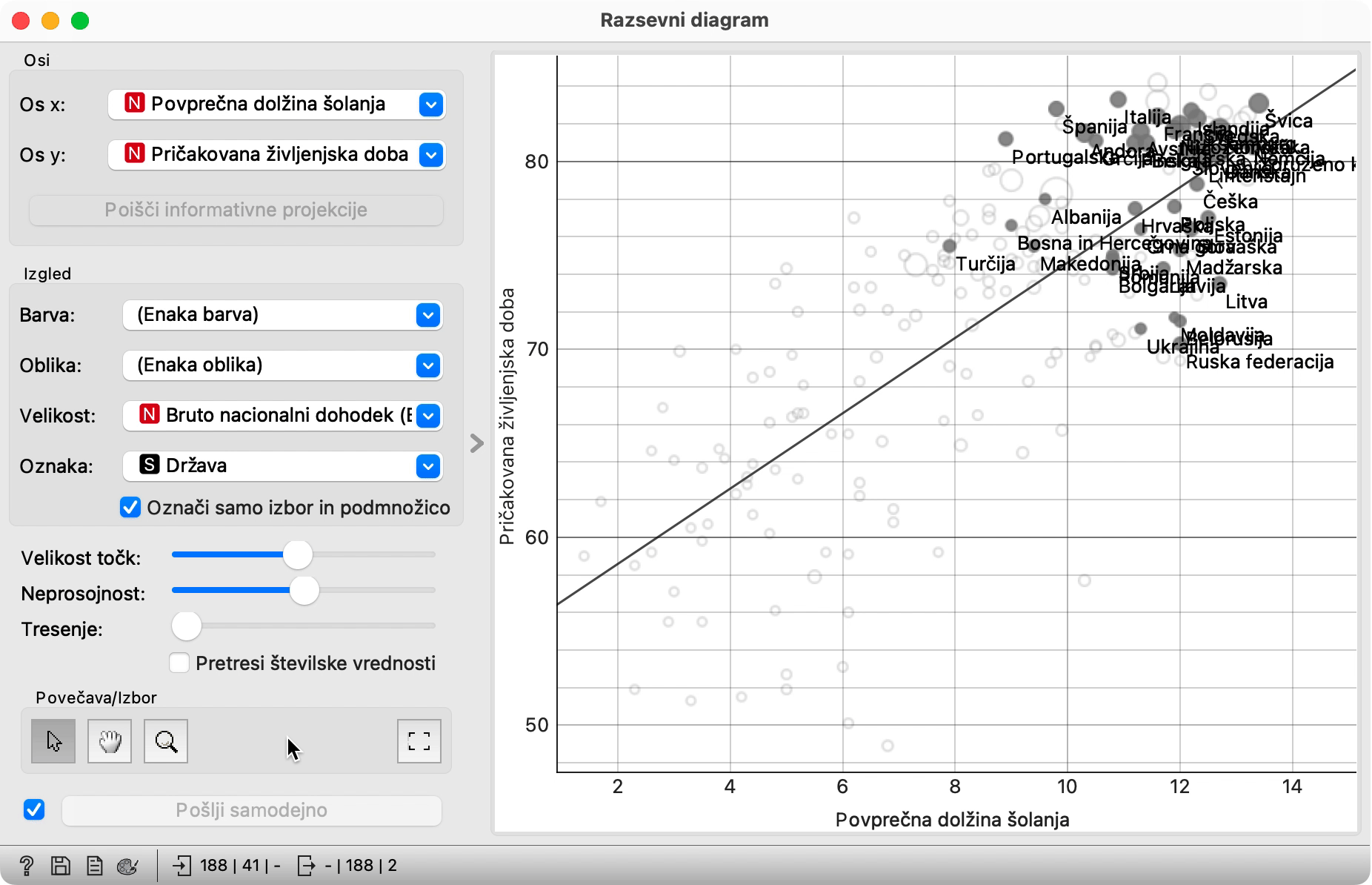 Pokaži ponovno
Pokaži ponovno
Kaj smo se naučili? Gradniki nimajo le več izhodov, temveč tudi več vhodov. Eden od njih je tipično privzet in ga Orange izbere prvega; ko dodajamo nove povezave, jemlje naslednje. Pri gradnikih, ki imajo le en vhod, pa bo nova povezava zamenjala obstoječo.
Vse bomo izvedeli, če dvokliknemo povezavo med Barvnim zemljevidom in Razsevnim diagramom.
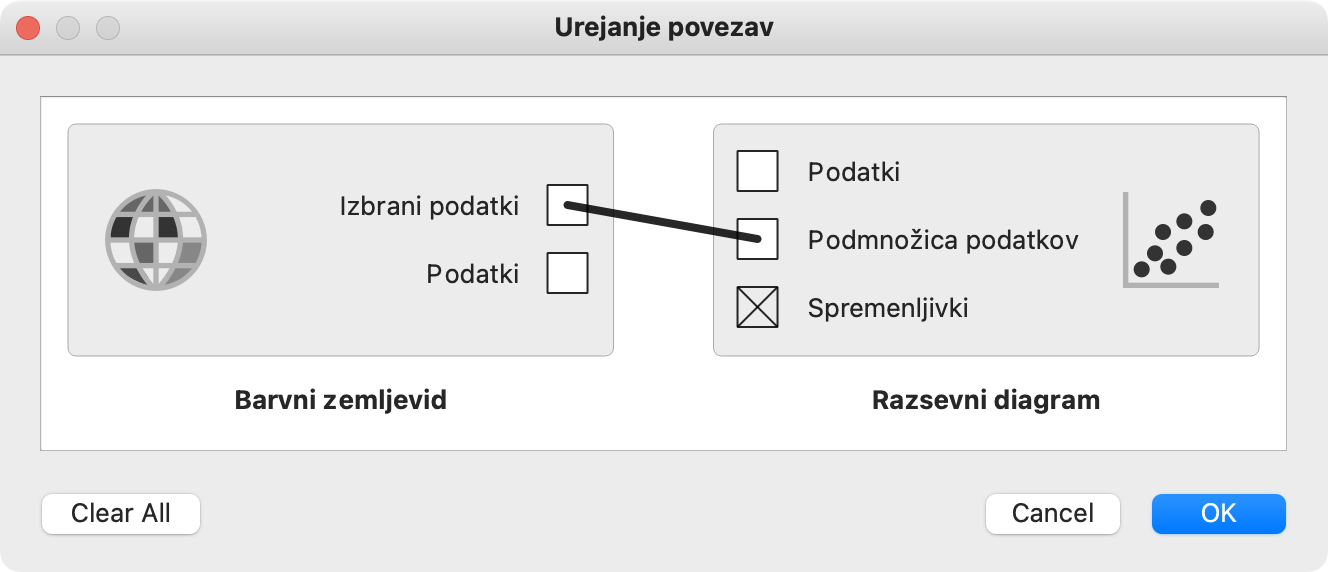
Barvni zemljevid ima, kot vemo, dva izhoda. Razsevni diagram ima tri vhode. Privzeti vhod so vsi podatki, naslednji so podatki, ki jih bo pokazal kot podmnožico, zadnji pa nas tule ne zanima, saj z njim (še) nimamo kaj početi.
V tem oknu lahko tudi preuredimo povezave, tako da jih preusmerimo iz drugih vhodov ali na druge izhode, če nam kaj ni všeč.
Tudi večina drugih gradnikov, ki kaže podatke, ima vhod s podmnožico podatkov.
Za vajo - ki nima kakega posebnega praktičnega pomena - narišite Razsevni diagram, v katerem bodo označene vse države, katerih ime se začne s črko S. (Namig: splača se uporabiti Tabelo.)
Da preverimo, kako vam je uspelo, poiščite vse države, v katerih se šolajo več kot 10 let in so pod črto. Koliko jih je?
Poglavje 9: Isto, a z manj šlamparije
... v katerem združujemo podatke iz različnih virov.
Tole poglavje bi lahko tudi preskočili, a pri pripravi podatkov za Pumice nam je prišlo tole pogosto prav. Zato le berite.
"Vse, kar se nahaja med Islandijo in Turčijo,« je bolj slaba definicija Evrope. Gotovo kaj manjka in gotovo je kaj preveč. (Že to, ali je Turčija res evropska država ali pa je bolj azijska, je vprašanje.) Kako bi to delo opravili točneje?
Kakorkoli brskamo po stolpcih, podatka o celini ni. Potem ga bo treba pač dodati. Za začetek si boste morali pripraviti tabelico z dvema stolpcema: v enem bodo države, v drugem njihove celine. Uporabite lahko, recimo, kako tabelo z Wikipedije ali kaj podobnega.
Šalim se. Tabelo smo vam že pripravili, kar shranite jo na svoj računalnik. Lahko si jo tudi ogledate v Excelu.
Da se ne zaplezamo, bomo gradnike postavljali od začetka. Pobrišite vse, razen Zbirke podatkov.
Zdaj pa bomo naložiti datoteko s celinami. To ne bo šlo z Zbirke podatkov, saj ta nalaga datoteke s spletnega repozitorija. Uporabili bomo gradnik Datoteka. Dodajte ga (recimo malo nižje kot Zbirke podatkov). Kliknite na tipko za odpiranje datoteke (mapica in tri pike) ter poiščite celine.xlsx.
Podatke lahko povlečete v Tabelo, da pogledate, kako so videti. Vendar ni videti nič posebnega: en stolpec z imeni držav in en s celinami.
Zdaj pa združimo obe tabeli v eno. Gradnik Združi vrstice sestavi dve tabeli v eno. Ena tabela je osnovna, druga pa vsebuje dodatne podatke za nekatere ali vse vrstice iz osnovne. V našem primeru je osnovna tabela ta, ki prihaja iz Zbirke podatkov, dodatni podatki pa iz Datoteka. Da se vse samo od sebe poveže pravilno, moramo najprej priključiti osnovno in nato dodatno tabelo. (Sicer pa bo treba dvoklikati povezave in prevezovati vhode in izhode.)
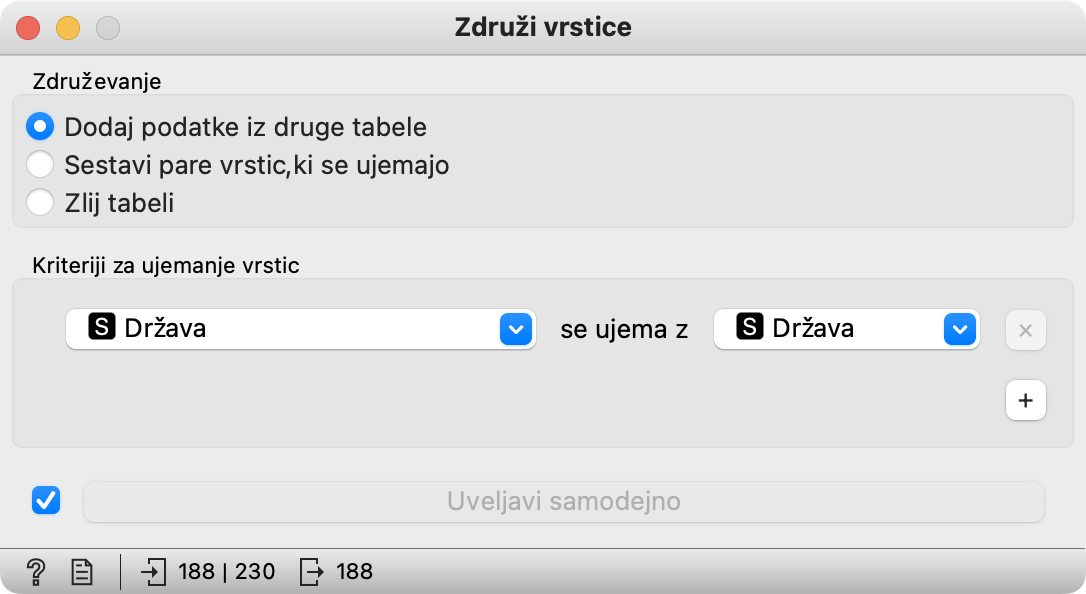
Tabeli sta urejeni različno. V celine.xlsx so države urejene abecedno, v osnovni tabeli pa naključno. Oranga to ne moti: ker imata obe tabeli stolpec Države, kar sam ugane, kako ju sestaviti. Če se imeni ne bi ujemali, pa bi morali ročno nastaviti stolpca, ki ju mora primerjati. Pomembno pa je, da so imena držav v obeh tabelah enaka. Če ena tabela vsebuje Češka republika, druga pa Češka, tega podatka ne bo znal povezati. Češki v tem primeru ne bi določil celine. Prav s tem boste imeli, če boste sami pripravljali podatke, največ dela.
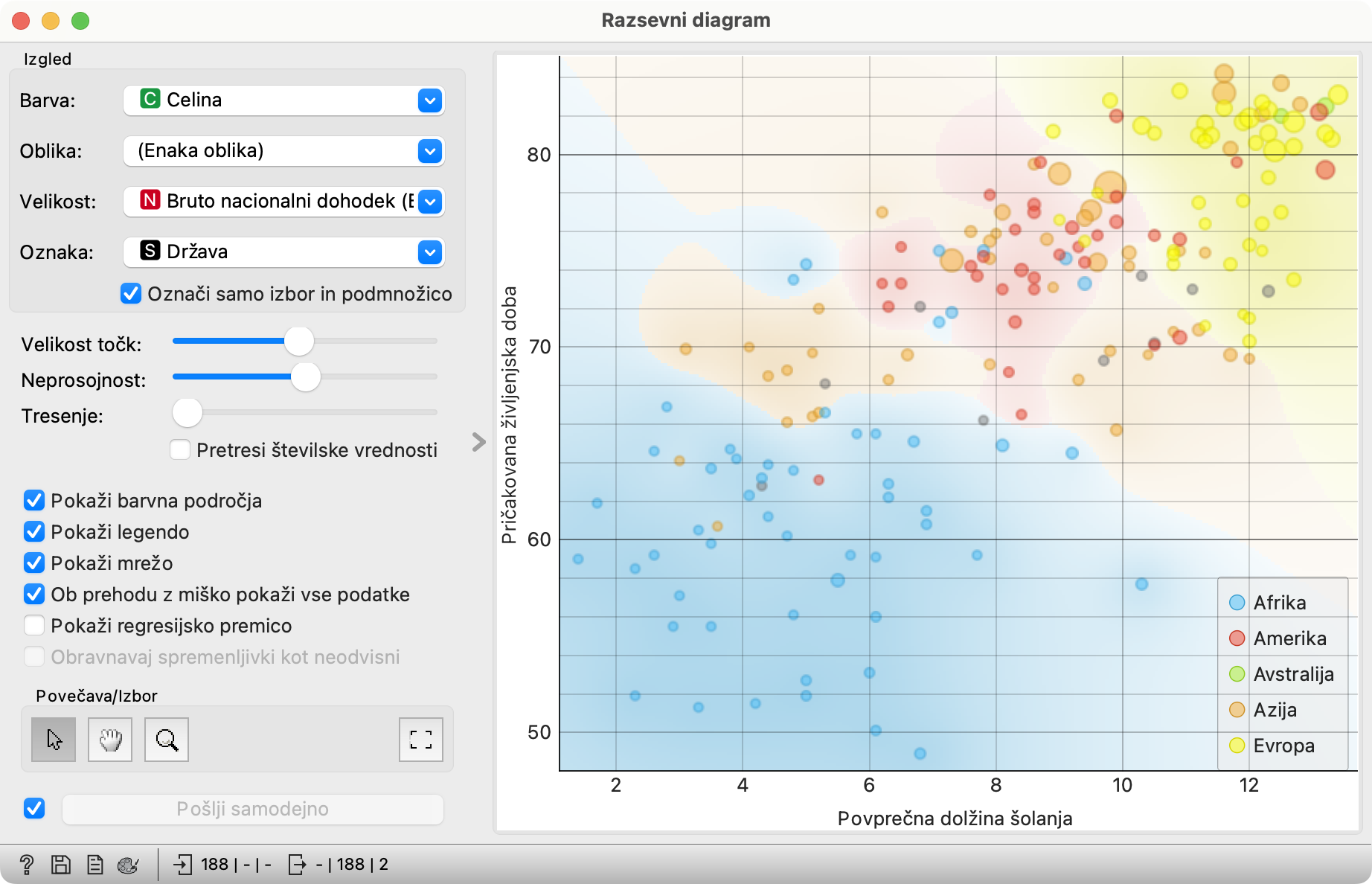
Povlecimo podatke iz Združi vrstice v Razsevni diagram. Pobarvajmo točke po celinah, pobrišimo kljukico pri Pokaži regresijsko premico, a izberimo Pokaži barvna področja.
Evropi gre pretežno dobro in Afriki pretežno slabo. Azija je raztresena povsod. Zanimiva pa je Amerika: ta je pretežno nad diagonalo, torej relativno dolgo življenje kljub kratki šoli. Če upoštevamo, da sta v severnem delu le dve državi (ZDA in Kanada), rdečih krogcev pa je veliko, je dolgo življenje v večini ameriških držav najbrž posledica sieste ter sambe in tanga.
Za odgovor na spodnje vprašanje bo potrebno uporabiti datoteko s podatki o porazdelitvi verstev (religije.xlsx). V njej je za vsako državo naveden delež populacije, ki pripada posamični veri (izbranih je le nekaj največjih verstev), večinska vera in njen delež.
V podatkih Svetovne banke ni Kosova, zato so štiri evropske države z največjim deležem muslimanov Albanija, Bosna in Hercegovina, Makedonija, Črna Gora. Katera je peta?
Podatki, ki jih uporabljamo v tem priročniku so že dopolnjeni: v izvirne podatke Svetovne banke smo dodali stolpca s koordinatami držav, saj bi jih bilo sicer težje postavljati na zemljevid.
Zdaj znamo dopolnjevati podatke, združevati podatke iz različnih virov. Prav pri pripravi podatkov za pouk nam bo prišlo to pogosto prav. Zato še zadnji detajl: z gradnikom Shrani podatke lahko zapišemo podatke v datoteko. Tule ga priključimo na Združi vrstice, pa si lahko enkrat za vselej shranimo dopolnjene podatke v datoteko in se izognemo združevanju v prihodnosti. Predvsem pa prihranimo to delo učencem.
Poglavje 10: Škatle z brki, politiki brez
... ker smo se že naveličali razsevnih diagramov.
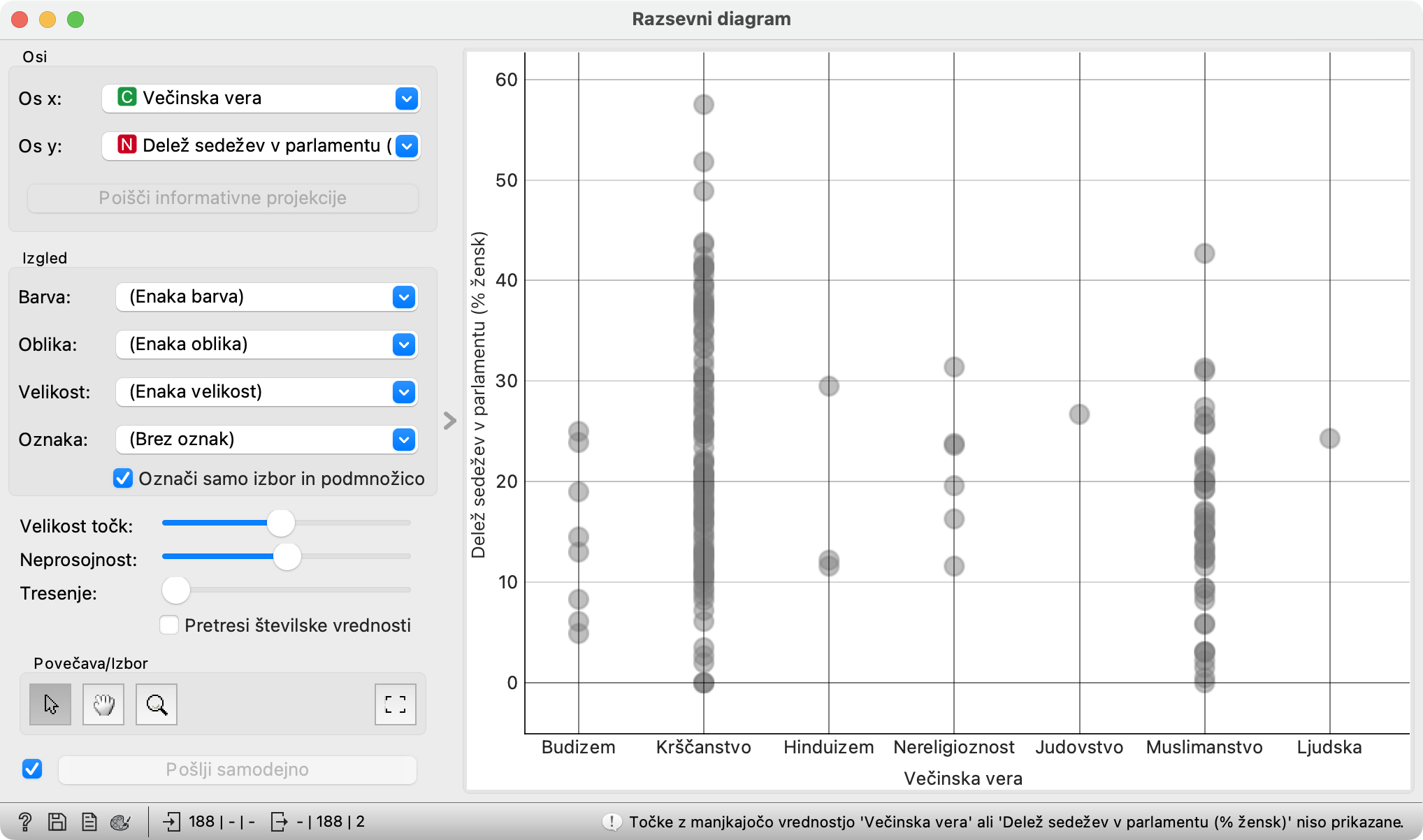
Naložimo dopolnjene podatke o državah (če si jih niste uspešno pripravili sami, lahko uporabite naše; naložite jih z gradnikom Datoteka). Potegnimo jih v Razsevni diagram in, za spremembo, za os x izberimo »Večinska vera« (večinsko vero vsake države) za y pa »Delež sedežev v parlamentu (% žensk)«.
Rezultat je videti drugače, kot smo vajeni. Razlog je v tem: doslej smo v razsevnem diagramu opazovali le številske spremenljivke, večinska vera pa je kategorična in ima eno od šestih možnih vrednosti. Zato njene vrednosti niso razpršene naokrog, temveč so zbrane na črti. (Da gre za drug tip spremenljivke vidimo tudi po tem, da pred njenim imenom ni rdečega N (numeric) temveč zelen C (categorical).)
S tem ni nič narobe, to je popolnoma uporabno. Še posebej, če povlečemo drsnik Tresenje malo na desno (poskusite!). Vidimo, recimo, da ima večina krščanskih držav v parlamentu nekje med 10 in 40 % žensk, v muslimanskih pa jih je manj, nekje do 30 %.
Katera država ima v parlamentu 57 % žensk?
Vendar je takšne podatke prikladneje risati drugače. V tem poglavju bomo spoznali prvi način, v drugem naslednjega.
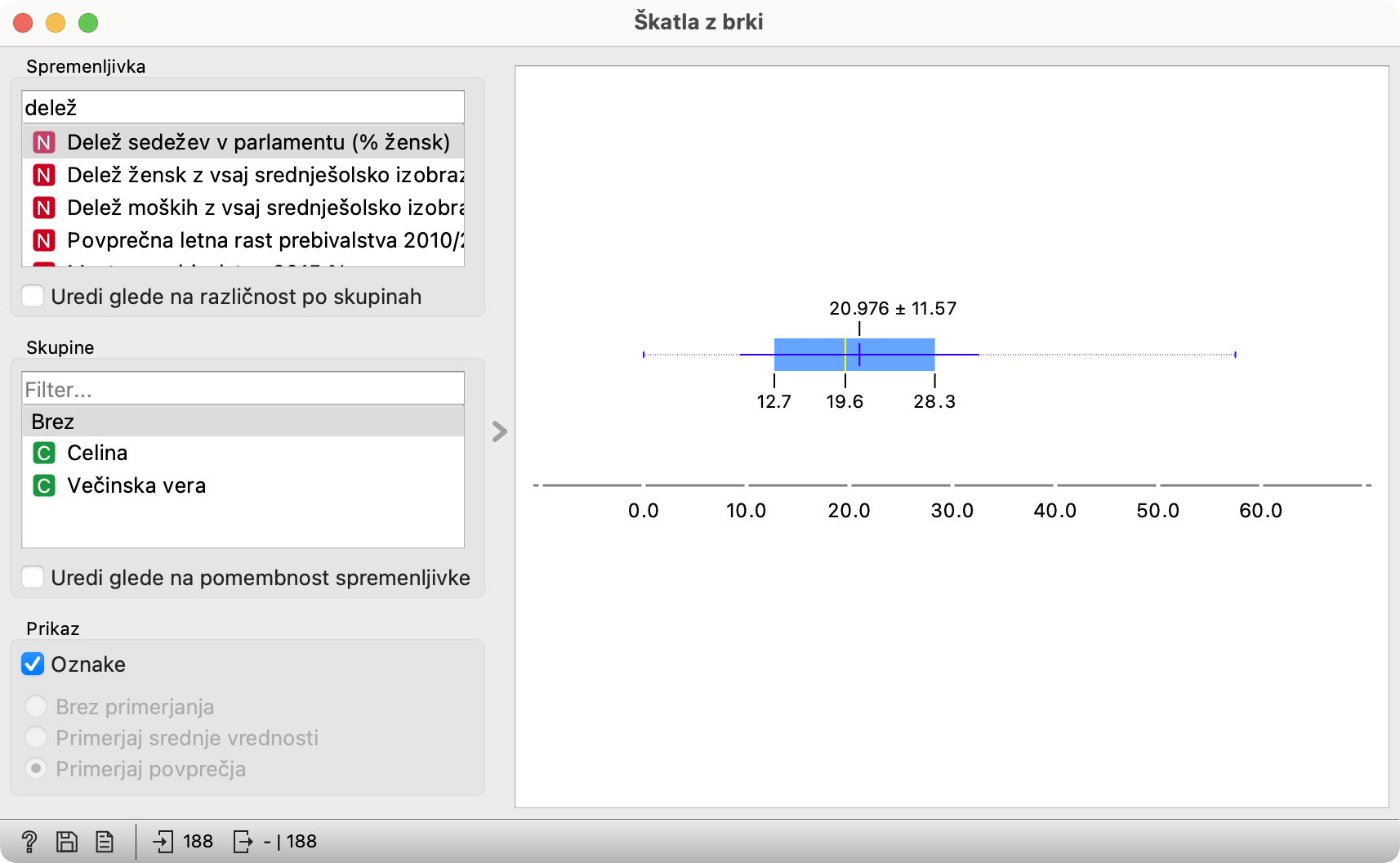
Angleži box plotu, pravijo tudi whisker plot ali, po naše, Škatla z brki. Spravimo podatke vanjo. Kot spremenljivko izberimo Delež žensk v parlamentu. Da jo lažje poiščemo, v polje »Filter« natipkamo del njenega imena, recimo »delež«.
Slika, ki jo dobimo, navduši vse, ki niso gojili previsokih pričakovanj.
Razlika med mediano in povprečjem je večja pri, recimo plačah. Večina ljudi ima podpovprečno plačo, ker posamezniki z ekstremno visokimi plačami dvigujejo povprečje.
Kljub njeni neimpresivnosti jo razložimo. Povprečni delež žensk v parlamentu je 20,976 %; tisti +- je standardni odklon; večji ko je, bolj se države razlikujejo. Spodaj najdemo mediano: polovica držav ima v parlamentu manj kot 19,6 % žensk, polovica pa več. Če se mediana in povprečje zelo razlikujeta, ima porazdelitev najbrž dolge repe - obstaja nekaj držav, ki zelo odstopajo navzgor ali navzdol. Tu ni tako: odstopanje je majhno, vseeno pa lahko razberemo, da ima več kot pol držav podpovprečno zastopanost žensk.
Splošno gledano: ti podatki so pravzaprav kar žalostni.
Številki levo in desno od mediane sta kvartila: četrtina držav ima v parlamentu manj kot 12,7 % žensk, le četrtina pa več kot 28,3 %.
Potem pa še brki: ti kažejo najmanjšo in največjo vrednost. Obstajajo ena ali več držav brez žensk v parlamentu in vsaj ena, ki ima v parlamentu skoraj 60 % žensk. Slednjo že poznamo, glede prvih pa vam moram zbuditi radovednost: če je kdo mislil, da imajo v tej državi člani parlamenta brade, bele halje in turbane, je zadel samo na četrt. Gre namreč za štiri države in le ena je večinsko muslimanska. Za katere države gre, boste brez težav odkrili sami, če le uredite tabelo po deležu žensk.
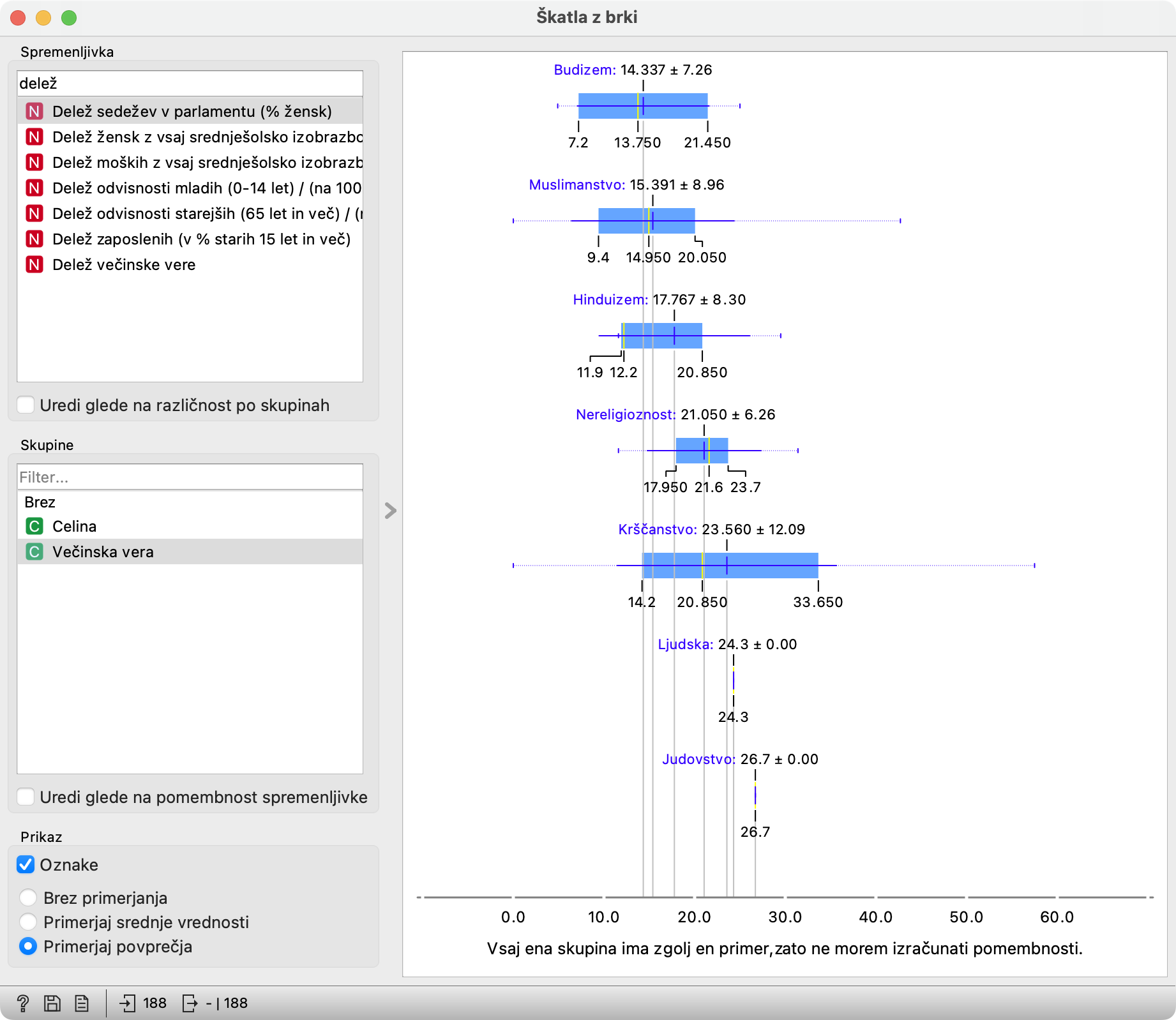
Prav, prav, ampak človek bi vseeno pričakoval - in pravzaprav je v prejšnjem poglavju človek tudi že videl - da muslimanske države praviloma vodijo ljudje z brki (in brado) in ne tisti brez. Seveda bi imel prav in prav takšnim primerjavam so namenjene Škatle z brki. Pod Skupine izberimo Večinska vera. (Pa še okno po potrebi povečajmo.)
No, tole je pa kar zanimivo: dobili smo enake škatle kot prej, le da imamo namesto ene same škatle sedem škatel, po eno za vsako večinsko vero. In vidimo: najmanj žensk najdemo v parlamentih budističnih držav, največ pa v krščanskih. Vidimo pa tudi, da se prav krščanske države med seboj najbolj razlikujejo (ker je škatla najširša).
Večinsko ateističnih držav je pravzaprav sedem (katere? poišči jih!), le da za eno (katero? poišči jo!) delež žensk v parlamentu ni zabeležen.
Pravzaprav ne. Največji delež žensk v parlamentu najdemo v večinsko judovskih državah. Pa tudi razlike med temi državami so najmanjše. Vendar to ni tako zanimivo, saj je takšna država le ena. Tudi da so razlike med večinsko ateističnimi državami majhne, ni čudno, saj jih je le šest.
Zdaj pa ste spet na vrsti vi.
Države katere celine imajo v poprečju najmanjši delež žensk v parlamentu?
V Franciji dejansko potekajo nasilni protesti prav v času, ko pišemo to besedilo, glede na njihovo pogostost pa je čisto verjetno, da potekajo tudi v času, ko ga berete.
Celin - tako kot tudi religij - seveda ne smemo obravnavati v kosu. Tako kot se japonskim turistom ni treba bati potovati v Evropo zaradi nemirov v Franciji (le Eifflovega stolpa letos pač ne bodo šli fotografirat), tudi Malezije, Kuvajta in Turčije ne gre enačiti. Za boljšo sliko - in mimogrede, da ponavljamo - izrišimo Barvni zemljevid tako, da bodo države obarvane glede na zastopanost žensk v parlamentih. (Namig: nastaviti je potrebno Vrednost.)
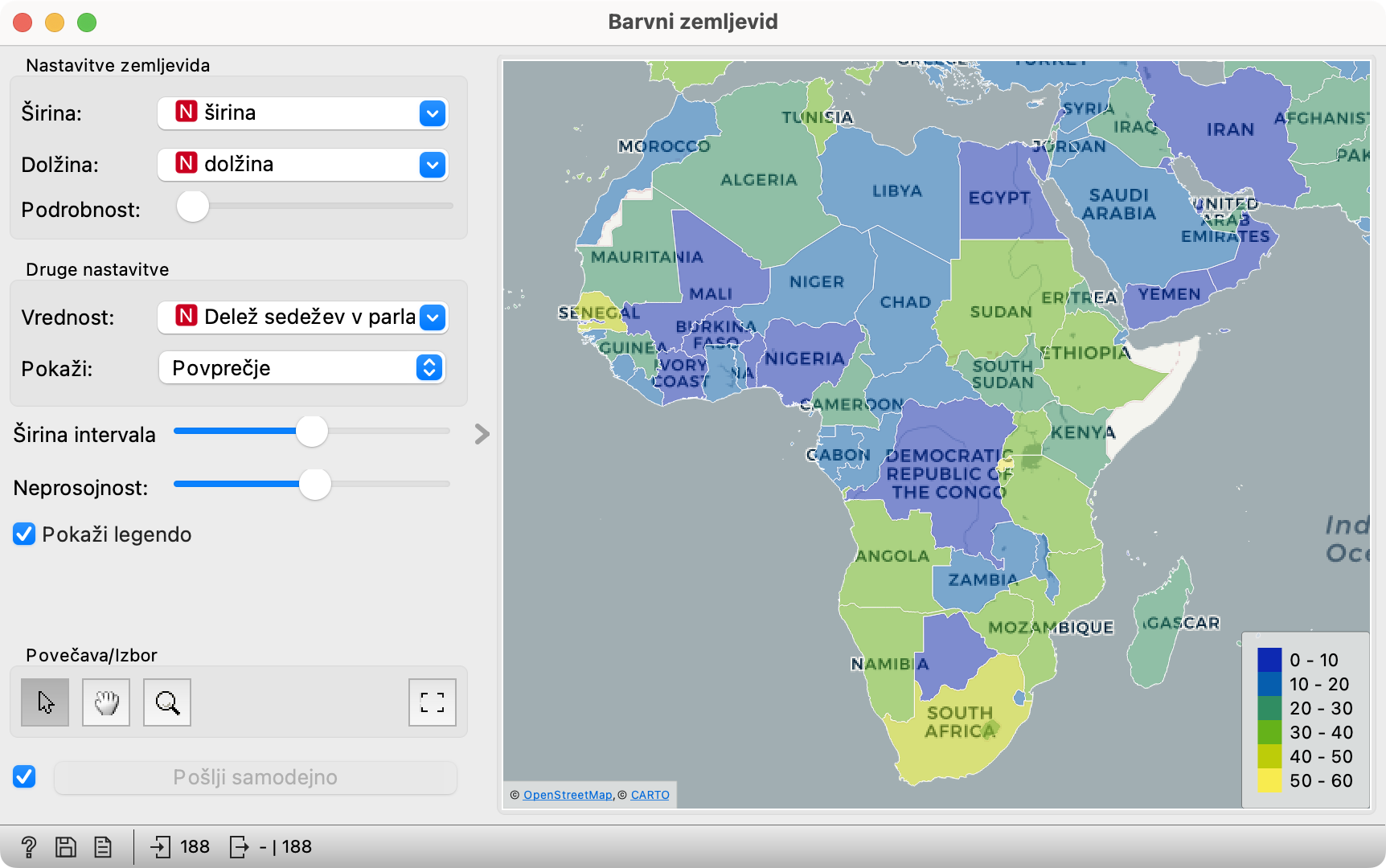
Med afriškimi državami predvsem štiri (pozitivno) izstopajo po deležu žensk v parlamentu. Ena je Južna Afrika, dve manjši in zato manj opazni sta Ruanda in Sejšeli. Katera je četrta?
Poglavje 11: Mi in oni
... v katerem bomo iskali razlike med različnimi skupinami.
Za stolpce smo začeli uporabljati ime »spremenljivka«. »Stolpec« je smiseln le, dokler si predstavljamo tabele. V različnih vedah bi to lahko bil tudi »kriterij« ali »lastnost«, v angleščini pa feature, attribute in še kaj.
Nemara se življenje na različnih celinah (v družbeno-ekonomskem smislu, ki ga pokrivajo ti podatki) vseeno ne razlikuje najbolj drastično ravno po številu žensk v parlamentih? Saj ne pravim, podatek je zanimiv, morda celo zgovoren in gotovo pomemben, ampak a ne bi šli počasi raziskovat še kaj drugega?
Podatki, s katerimi bomo delali, so še vedno dopolnjeni podatki o državah, kot v prejšnjem poglavju.

Ko smo iskali podatek o deležu žensk v parlamentih, smo v vrstico »Filter«, ki je nad škatlo s spremenljivkami, napisali del imena spremenljivke. Pobrišimo ga, da bomo spet videli vse. »Skupine« naj bodo Celina. Zdaj kliknemo eno od spremenljivk, na primer kar prvo (Pričakovana življenjska doba; zemljepisna širina in dolžina nista tako zanimivi, saj vemo, da je Evropa večinoma zgoraj in Avstralija večinoma spodaj). Potem lahko gremo prek različnih spremenljivk kar tako, da pritiskamo tipki gor in dol.
Po nekaterih kriterijih se celine razlikujejo bolj, po drugih manj. Spremenljivk je veliko in iskanje zanimivih bo dolgo. Nam ne bi mogel pri tem pomagati računalnik?
Obkljukajte »Uredi glede na različnosti po skupinah«. Spremenljivke so zdaj urejene glede na to, kako se njihove vrednosti razlikujejo po skupinah. Izkaže se, da se celine najbolj razlikujejo po tem, kje so; Amerika je levo, Avstralija desno. Očitno in nezanimivo. Veliko zanimivejša, pomembnejša, zaskrbljujoča je naslednja lastnost na spisku.
Izvzemši zemljepisno dolžino, po kateri lastnosti se države na različnih celinah najbolj razlikujejo?
Pri izražanju smo tule malo nenatančni. Ne gre za polovico prebivalstva. Pravilneje bi bilo reči »v polovici evropskih držav je povprečna starost prebivalstva večja od 41«. Enako velja za druge kriterije, o katerih bomo govorili v nadaljevanju.
Kdor je rešil nalogo, je odkril sam. Temu, ki je ni, bomo izdali odgovor. Da, Evropa je stara. Povprečna starost in mediana sta približno 41. Polovica prebivalstva Evrope je starejša od 41 let. In polovica Afrike mlajše od 18,7.
Če rečemo, da je polovica prebivalstva starejša od 41 let, govorimo o povprečju ali mediani?
Tole je pač druga plat tega, da v Evropi živimo dlje. Le pobrskajmo po spremenljivkah, Pričakovana življenjska doba se tudi zdaj, ko so spremenljivke urejene po različnosti glede na celine, ni umaknila prav daleč dol po spisku.
Spet: ne pozabimo, da opazujemo poprečja državnih poprečij. To ni nujno povprečje za celotno Afriko ali Evropo. Če v državah z več prebivalci živijo dlje, je povprečje za celino višje, kot ga vidimo tu.
Za koliko let (brez decimalk) se razlikuje poprečna pričakovana življenjska doba Evropejca in Afričana?
V živalskem svetu je lahko povezava celo obratna: kjer se rodi preveč mladičev, ni dovolj prostora in hrane za vse, zato preživijo le ptički, ki najširše odpirajo kljune in najuspešneje izrinejo iz gnezda ostale. Še več, imeti preveč mladičev, da pride že v gnezdu do izbora, je del sistema.
Faktorji so seveda še drugi, reč je kompleksna. K postaranosti Evrope prispeva tudi nizka rodnost, nizka rodnost pa je povezana z dolgim življenjem. Ali, še verjetneje, obratno, kjer umre veliko otrok, je potrebno povečati njihovo produkcijo. Kruto, a tako je.
Kakšno je poprečno število otrok na žensko v Afriki?
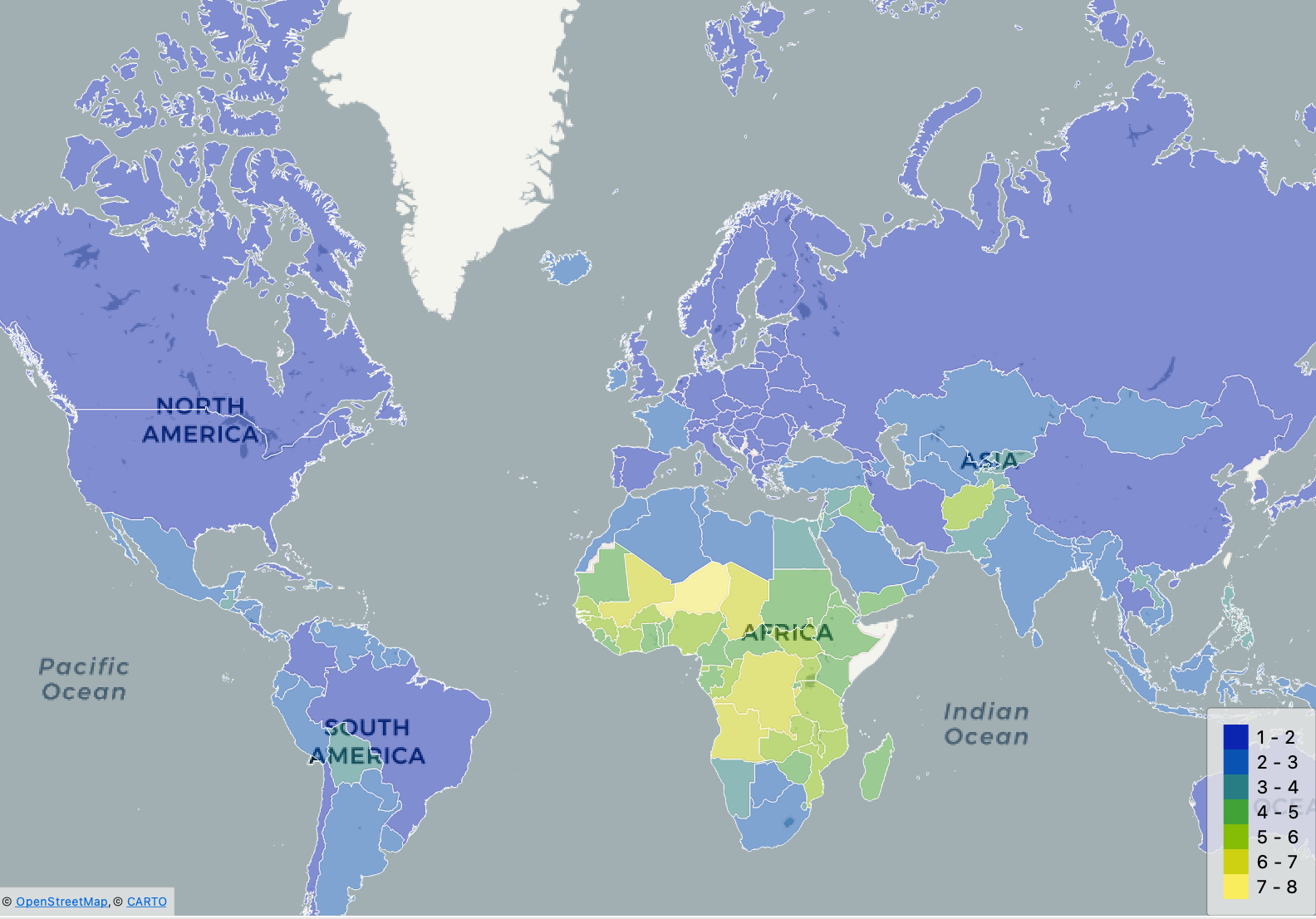
Da, rezultat za Afriko je kar velik, a glavobolen je pogled na Evropo: v letih 2000-2007 je povprečna Evropejka (povprečje povprečij prek držav) rodila 1.5 otroka.
Ob koncu prejšnjega poglavja smo zapisali, da niso vse države na vseh celinah enake. Najbrž to velja tudi za rodnost po Evropi? Na zemljevidu sveta Evropa ni videti rožnato, temveč bolj ali manj temno modro.
To je posledica skale: ker v neki afriški državi (kateri?) pravzaprav malo pretiravajo (halo? 7.6! V poprečju!), so praktično vse evropske države stisnjene v isti koš. Da bomo lahko smiselno primerjali evropske države, izberimo le njih.
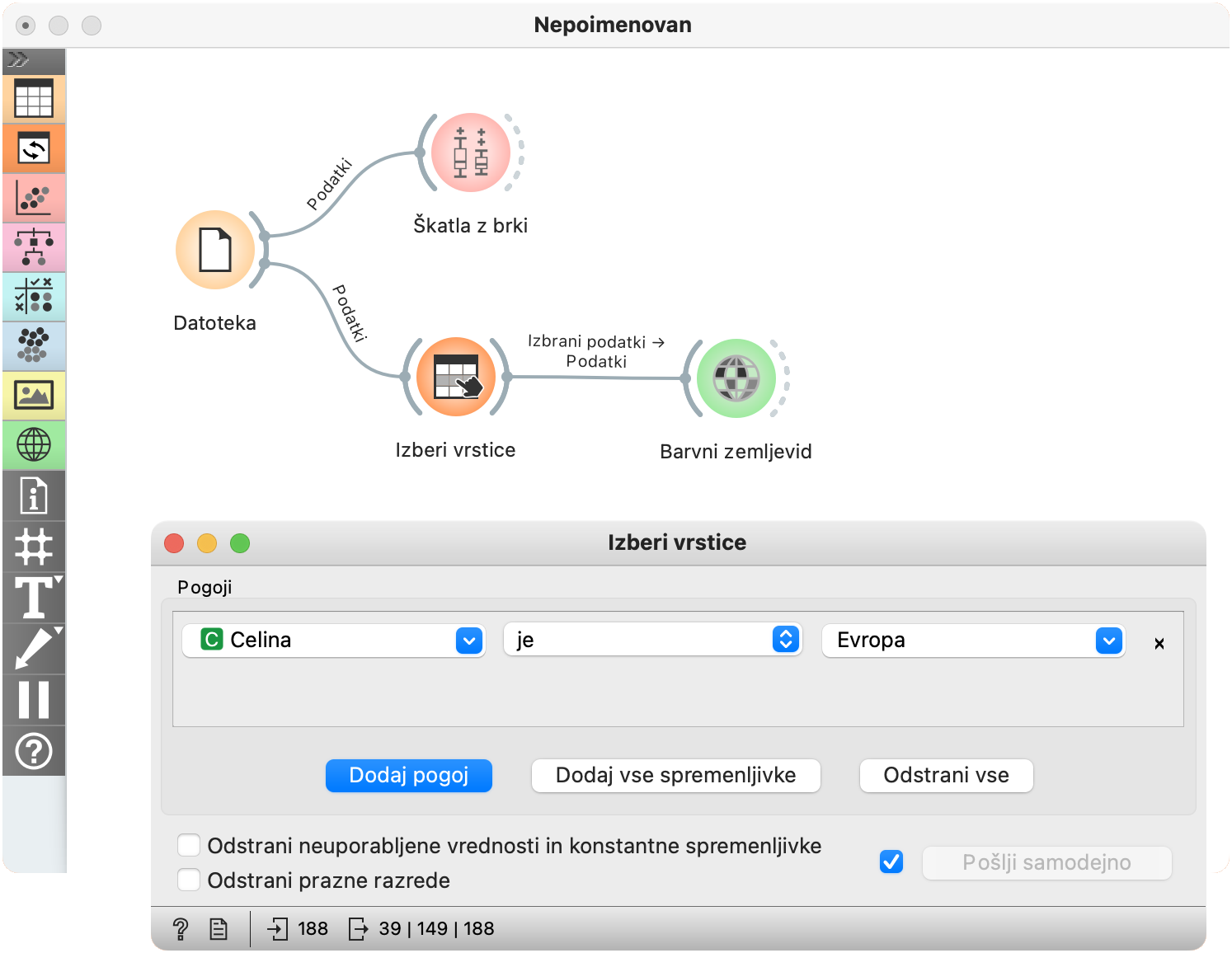
Da ne bi za izbiranje vedno uporabljali Tabele, končno - pa čeprav na hitro - spoznajmo namenski gradnik: Izberi vrstice.
Kaj počne, je očitno: dobi podatke, jih prefiltrira glede na podani kriterij ali kriterije in na izhod da, kar ostane. Kriterij je lahko tako preprost kot tu (Celina naj bo Evropa), lahko pa postavimo cel seznam (zanimajo nas afriške države, v katerih je rodnost vsaj 4 in je delež žensk v parlamentu znan).
Če obkljukamo Odstrani neuporabljene vrednosti in konstantne spremenljivke, bo odstranil spremenljivke, ki po filtriranju povzročajo samo še navlako. V tem primeru je to stolpec Celina, saj imajo vsi izhodni primeri isto vrednost, Evropa.
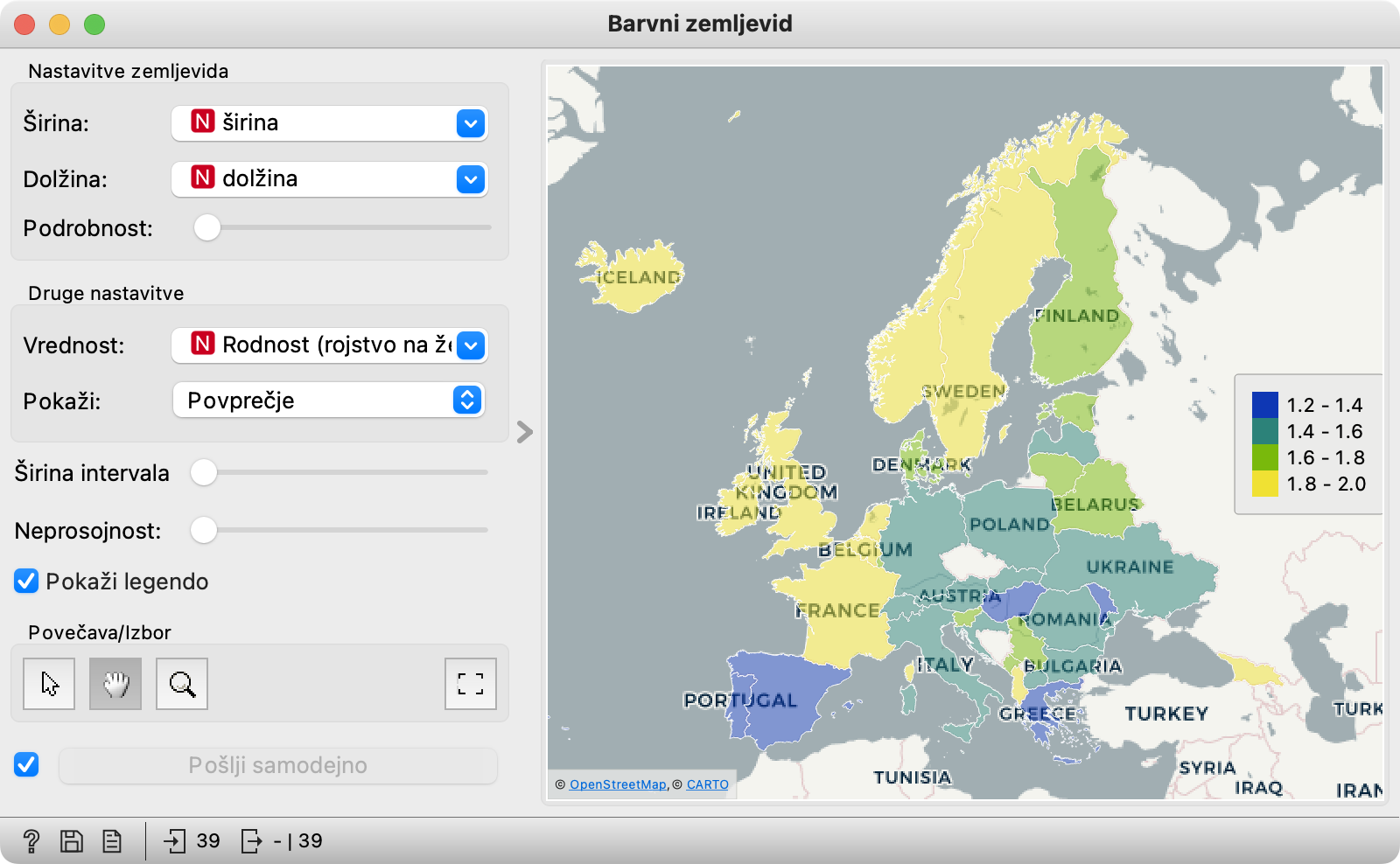
Spodbudneje? Malenkost. Očitno obstajajo države, katerih prebivalstvo se bo redčilo počasneje kot v drugih.
Preden zaključimo, poglejmo povezavo med rodnostjo in starostjo še z razsevnim diagramom. Na eno os damo pričakovano življenjsko dobo, na drugo rodnost, za dodatno informacijo pa države še obarvamo glede na celino.
S slike lahko razberemo veliko: res gre za obratno sorazmerje, vendar ne nujno (oziroma najbrž sploh ne) direktno vzročno povezavo. Veliko verjetneje je, da imata obe lastnosti zgolj nek skupni vzrok. V razsevnem diagramu se tudi lepo vidi, kje je (pretežno) Afrika, kje Evropa in kako so razporejene države vmes.
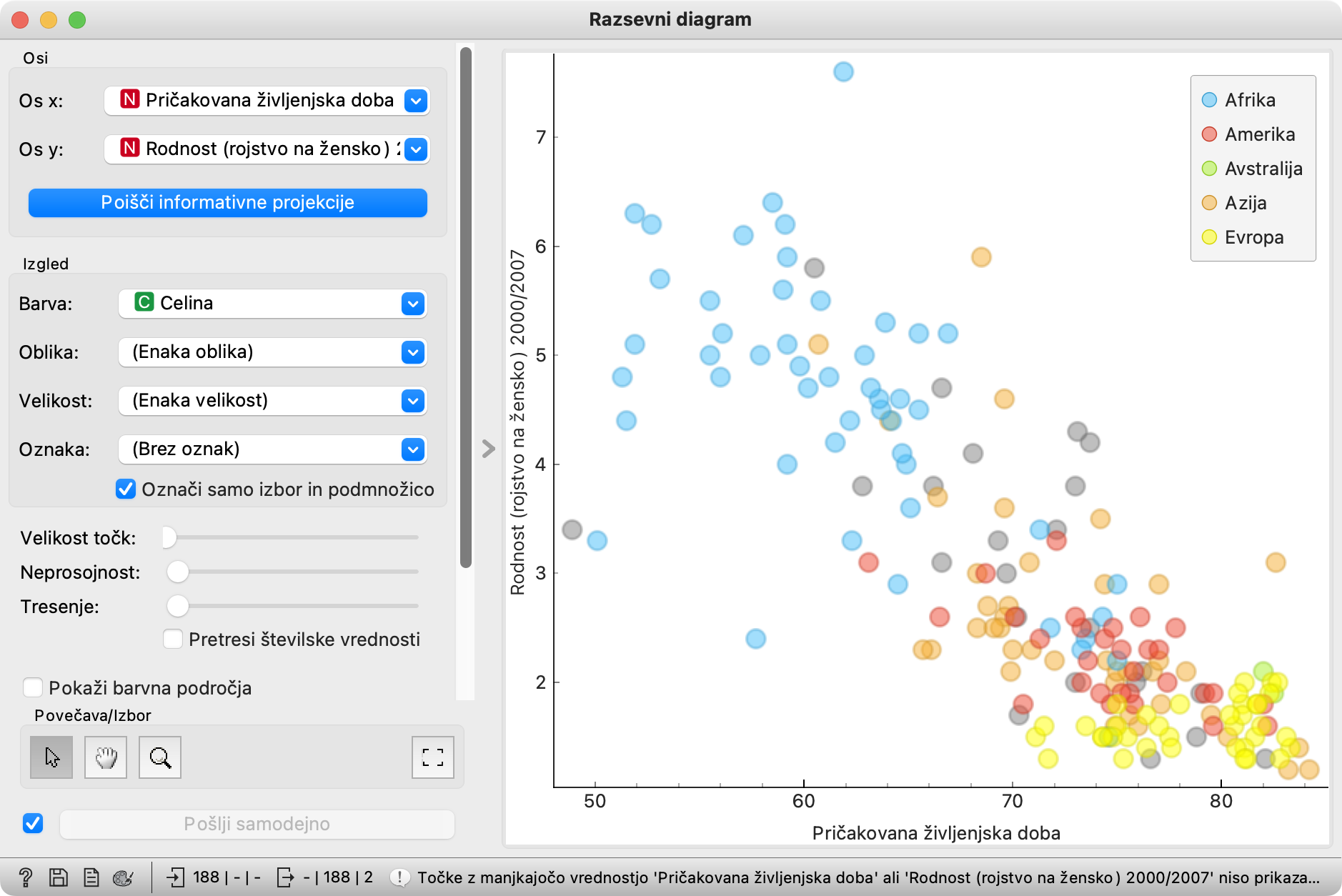
Hm, rekli smo »s slike lahko razberemo veliko«. Da, v tem poglavju smo spoznali močno orodje, ki je očitno lahko zelo uporabno tudi v razredu. Škatle z brki nam omogočajo iskati in opazovati razlike med skupinami. Tule med državami na različnih celinah, pri biologiji pa morda med neko lastnostjo živali v različnih živalskih vrstah - ali pri isti živalski vrsti, a v odvisnosti od tipa naravnega okolja. Dodatno lahko razlike osvetlimo z Razsevni diagrami. Paziti pa moramo, da s slike ne razberemo preveč. Zato je čas, da se v naslednjem poglavju ustavimo in posvarimo.
Poglavje 12: Teksaški ostrostrelec
... ki nas svari pred prenagljenim sklepanjem.
Teksaški ostrostrelec najprej strelja v lopo in nato nariše tarčo tam, kjer so luknje najgostejše.
Naj, če mu je v veselje. Od parih lukenj se lopa ne bo podrla. Hujše je, ko strelja v podatke. Tam vzame dve skupini, za kateri ni prav nobenega razloga, da bi se razlikovali po čem bistvenem. Recimo, da si prostovoljce za svojo študijo nabere tako, da gre za dva dni v Maribor ustavljat sprehajalce ob Dravi. Razdeli jih v dve skupini, namreč »sredini« in »četrtkovi«; recimo, da jih je v vsaki skupini dvajset. Vsak od teh revežev mu izpolni vprašalnik s stotimi vprašanji.
Doma analizira rezultate … in v svoje veliko presenečenje odkrije, da imajo tisti, ki gredo na sprehod ob sredah bistveno raje palačinke s čokoladno kremo, za razliko od četrtkovih, ki jih ne marajo. Z bistveno mislim bistveno: na skali od 1 do 10 je bilo sredino poprečje 8.4, četrtkovo pa 3.2!
Saj vidimo, zakaj gre za isti problem kot pri streljanju v lopo? Če primerja dve skupini po sto kriterijih, ni vrag, da se ne bosta po enem slučajno razlikovali. Statistik vam zna te stvari tudi poračunati: verjetnost, da najde razliko, ki je večja od toliko in toliko, je odvisna od tega, koliko stvari opazuje in kako velike so skupine.
Seveda lahko - in pravzaprav najbrž moramo - odmahniti z roko. Dokler ne slišimo razlage, kako naj bi bil dan sprehajanja povezan z najljubšim nadevom za palačinke, nam v povezavo ni potrebno verjeti. Če bo možakar najedal in nam mahal pred nosom s števillkami, pa ga preprosto prosimo, naj svojo akcijo ponovi še naslednjo sredo in četrtek ter prinese rezultate. Zelo malo verjetno je, da ga bomo še kdaj videli.
Škatle z brki, konkretno njihova zmožnost, da nam pokažejo spremenljivke, po katerih se skupine najbolj razlikujejo, so avtomatizirani teksaški ostrostrelec. Teksaška brzostrelka. (Mimogrede, znajo tudi obratno: izberemo lahko spremenljivko in uredimo skupine, Uredi glede na pomembnost spremenljivke.) To ne pomeni, da jih ne smemo uporabljati, temveč le, da moramo to, kar nam pokažejo, jemati kot namig o možni povezavi (ki pa je lahko tudi naključna) in ne kot dejstvo.
Podobne opcije, ki nam pomagajo iskati možne povezave, imajo tudi drugi gradniki Oranga in druga orodja za analizo podatkov.
Pa statististični testi? Se to ne reši s statističnimi testi? P-vrednosti pa te stvari? Ne, in razlog je pravzaprav prav zanimiv: statistični testi nam ne bodo pomagali prav zato, ker Škatla z brki ureja spremenljivke natančno po njihovih p-vrednostih. Uredi jih prav po tem, kako močno statistični testi potrjujejo razlike.
Avtorji Oranga, ki takorekoč programiramo to »statistično brzostrelko«, o tem veliko razmišljamo in pišemo. Nekaj krajšega je v prispevku How to abuse p-values in correlations, daljše (a, verjamemo, tudi lepo berljivo) besedilo, ki pojasni, kako delujejo statistični testi in zakaj nam ne morejo tule prav nič pomagati, pa je Carrots, Horses and Fear of Heights.
Če se vam ne ljubi brati, pa vas le ponovno posvarimo: za vzorce, ki jih najdemo v podatkih, mora obstajati tudi neka smiselna razlaga. Le tedaj smo lahko vsaj malo prepričani, da najdeni vzorec ni naključen in ne rišemo tarče okrog strela.
Poglavje 13: Škatle z brki brez brkov
... ki pravzaprav niso brkate škatle, temveč kažejo porazdelitve.
Vrnimo se k Škatlam z brki. Skupine so še vedno Celine, kot spremenljivko pa izberimo … Celine! To zveni kot dokaj neumna ideja: očitno bomo izvedeli, da so vse afriške države v Afriki, evropske pa v Evropi. Ampak vseeno ubogajte. Ne bo tako neinformativno; pomagalo vam bo odgovoriti na naslednje vprašanje.
Eno PTSD doživetij avtorja tega besedila je osnovnošolska kontrolka, v kateri smo morali v zemljevid te celine vpisati imena vseh držav. Globoko v kleti Bloomove taksonomije!
Na kateri celini je največ držav?
Vse, kar bomo narisali v tem poglavju z Brkatimi škatlami, bi lahko tudi s Porazdelitvami, le da je tu vodoravno, tam pa bi bilo navpično.
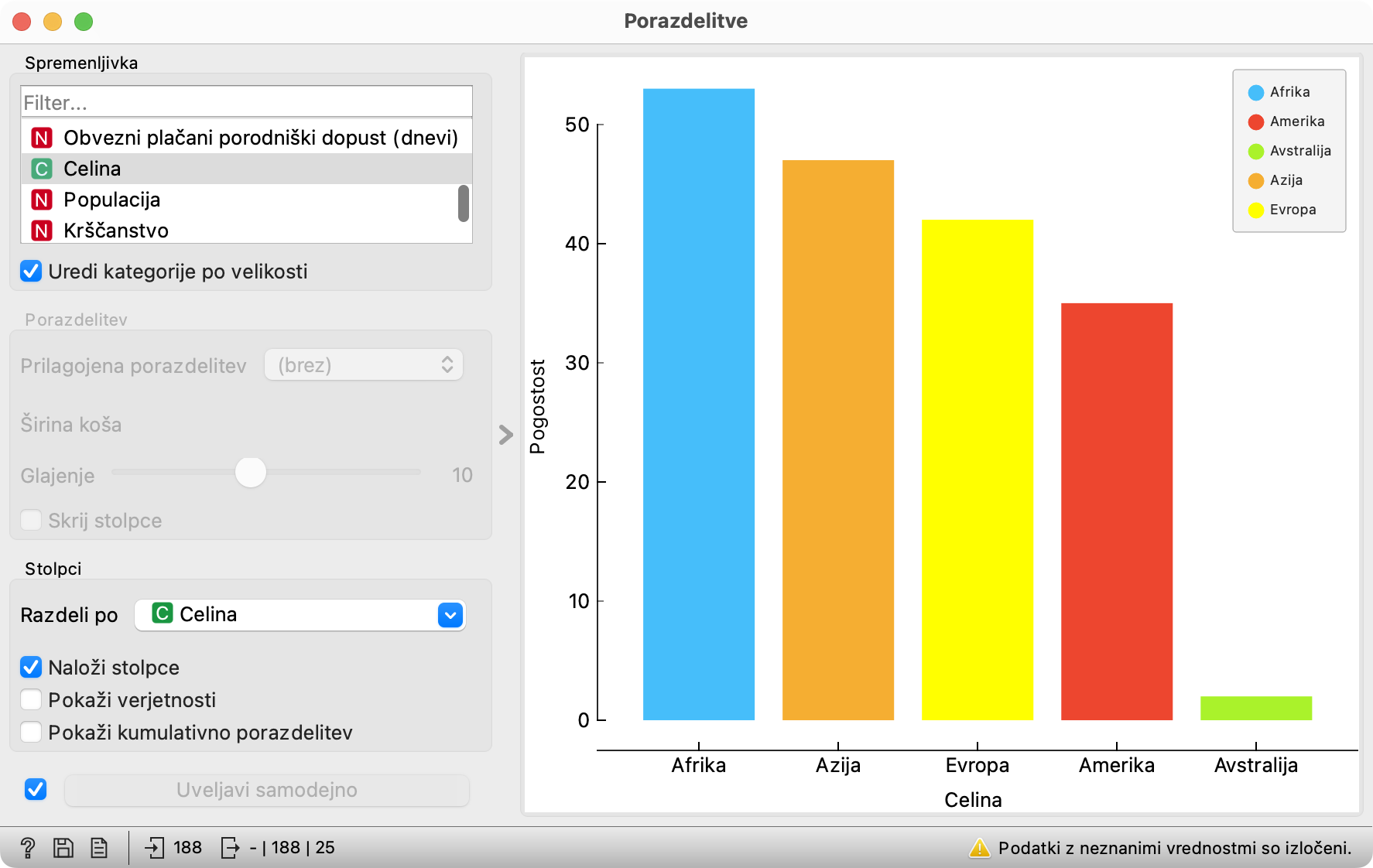
Zdaj pa kot spremenljivko namesto Celine izberimo večinsko vero.
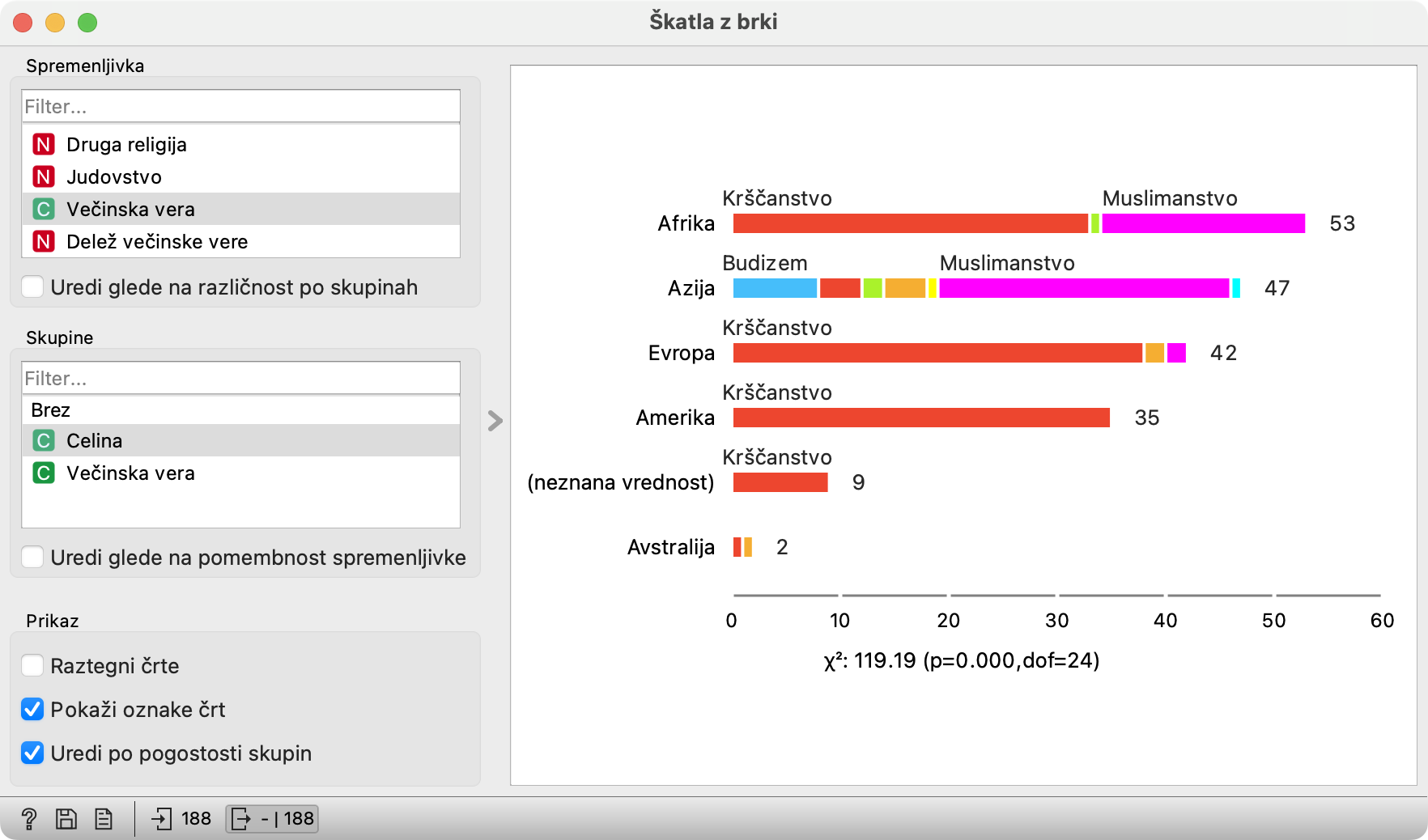
Dolžina afriške škatle je ustrezala 53 državam, dolžina - recimo - ameriške pa 35. Zdaj je vsaka od teh škatel razdeljena glede na večinske vere. Afriških 53 se je razdelilo na 33 krščanskih, 1 hindujsko in 19 muslimanskih. Pardon? Eno hindujsko? V Afriki? Katera?! In, pravzaprav, odkod nam številke?
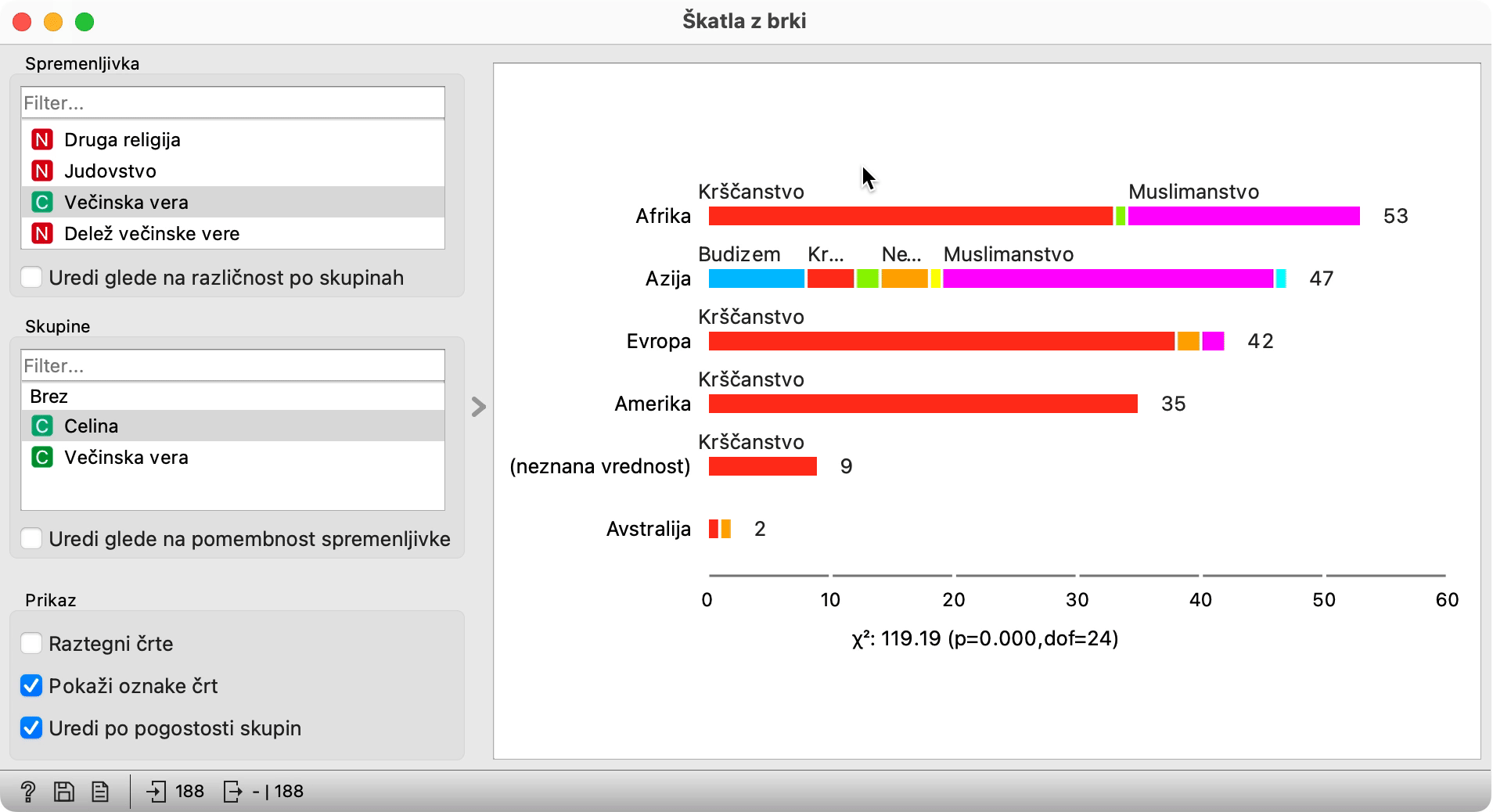
Iz gradnika Škatla z brki, kajpada. Če postojimo z miško nad škatlo, izvemo nekaj o njej. Če kliknemo nanjo, pa gredo pripadajoče države na izhod, kjer jih lahko pregledujemo v nadaljnjih gradnikih, ali pa poškilimo v tabelo kar v predogledu.
V istem gradniku se lahko poučimo tudi o deležih. Izberimo Raztegni črte in vse škatle bodo postale enako dolge. Mimogrede se spremenijo tudi oznake - številke pod škatlami. Prej so šle do 53, kolikor je največje število držav na celini. Zdaj gredo do 100 in pomenijo odstotke.
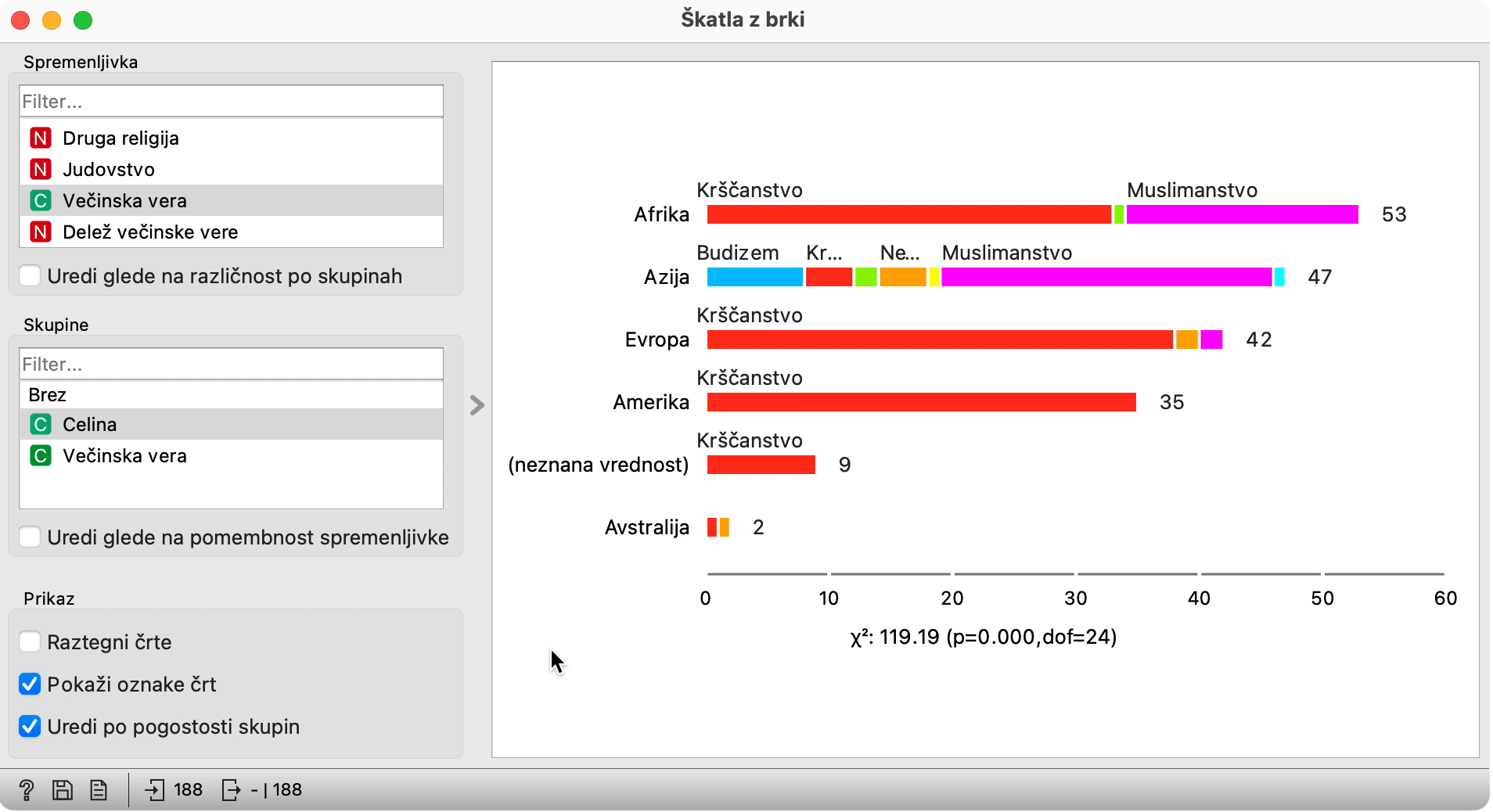
Če smo prej izvedeli, da imajo v Afriki hindujci večino v eni državi od petdesetih, zdaj vidimo, da je večinsko hindujskih 1.89 % afriških držav. To ni čisto isto: na prejšnji sliki smo s primerjavo velikosti (pod)škatel primerjali število držav s posamezno večinsko religijo, na tej pa primerjamo deleže držav.
Katera celina ima torej največji delež (večinsko) krščanskih držav?
Vprašanje je (popolnoma namerno) postavljeno dvoumno. Kaj nas pravzaprav zanima?
- Če vzamemo neko celino, se lahko vprašamo, kakšen delež držav na njej je (večinsko) krščanskih.
- Če vzamemo vse (večinsko) krščanske države, se lahko vprašamo, na kateri celini je največji delež od njih.
Razumemo? Enkrat gre za deleže celin (ki sodijo v posamezno religijo), drugič gre za deleže religij (ki so na posamezni celini). Razlika je zelo pomembna in nanjo naletimo povsod. Enkrat gre za to, koliko Butalcev je neumnih, drugič pa zato, koliko neumnežev se je naselilo v Butale. No, resno, enkrat gre za to, koliko cepljenih zboli za kovidom, drugič pa za to, koliko obolelih je cepljenih. Očitno gre za različne stvari: delež cepljenih, ki zbolijo, je odvisen od kvalitete cepiva (in nalezljivosti bolezni), delež obolelih med cepljenimi pa je očitno odvisen (tudi in predvsem) od tega, kolikšen delež populacije je cepljen. Delež odličnjakov med dekleti je na tehničnih šolah bistveno večji od deležev deklet med odličnjaki - preprosto zato, ker na tehničnih šolah ni veliko deklet.
Kaj torej kažejo gornje brkate škatle? Vsako celino razdelijo glede na verstva, torej kažejo, kolikšen delež držav na posamični celini je večinsko krščanski. Če se vprašamo, kakšna bo večinska vera v neki ameriški državi: krščanska. Če vzamemo krščansko državo, pa ne bo nujno v Ameriki. Da bi odgovorili na to, drugo vprašanje, moramo zamenjati vlogi spremenljivk: risati moramo religije in jih razdeliti po celinah.
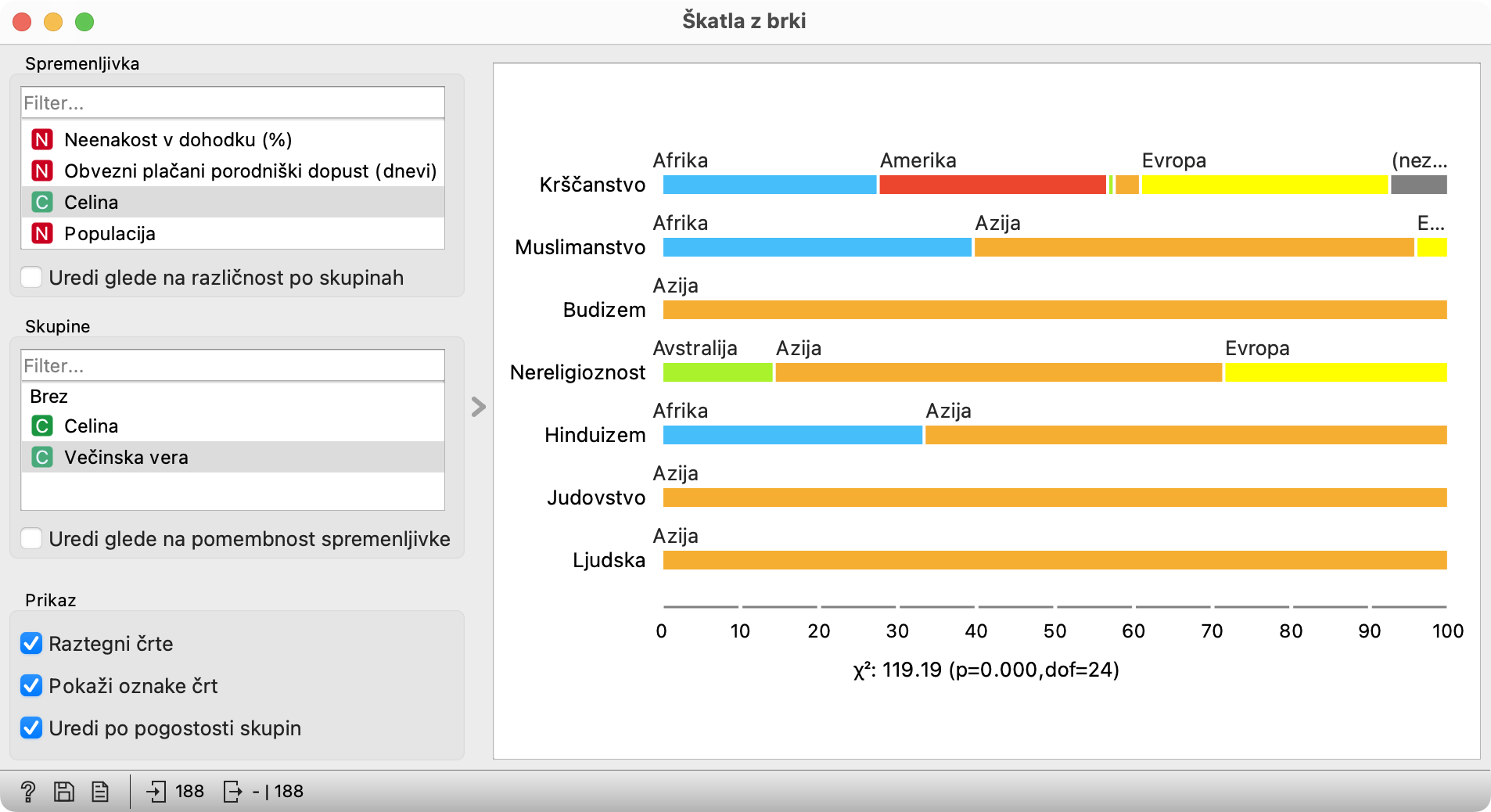
Krščanske države so enakomerno razdeljene po Evropi in Ameriki (38 in 35 držav oziroma 31.67 % in 29.17 % na vsako - in ne na vsaki!). Vidimo tudi, da so vse budistične države v Aziji, ob čemer seveda vemo, da niso vse azijske države budistične. (Že zato, ker so tudi vse judovske države v Azije, ne da bi bila vsa Azija judovska.)
Samo še preprosto vprašanje za konec, da boste morali še malo prenastavljati gradnik.
V koliko državah je večinska vera islam?
Tako. Zdaj poznamo osnovne vizualizacije - Porazdelitve, Razsevne diagrame in Škatle z brki - in če jih znamo dobro povezovati in obračati, se lahko z njimi že kar dobro poglobimo v podatke. V naslednji knjigi se bomo potopili globlje v analizo podatkov: v sestavljanje modelov.