Napovedni modeli: Klasifikacijska drevesa

Poglavje 1: Uvod

Dobro se spomnim, kako nam je, študentom računalništva, prof. Ivan Bratko definiral umetno inteligenco. Rekel je, da jo je težko jasno definirati, zato najraje rečemo, da je neka stvar (program, računalnik...) »umetno inteligentna«, kadar imitira človeško inteligenco. S svojim značilnim nasmehom je dodal, da tako prepustimo definicijo psihologom.

Raziskovalce umetne inteligence je torej že po definiciji vedno zanimalo oponašanje veščin, ki jih imamo ljudje — no, vsaj tisti, ki smo inteligentni. :) Ena od njih je napovedovanje.

Vzemimo kmeta iz Vipavske doline, ki se je pred sto leti pripravljal h kakemu opravilu, katerega uspešnost je bila odvisna od vremena v prihodnjih dneh. Tudi brez radijske vremenske napovedi je dobro vedel, kako je vreme pojutrišnjem odvisno od tega, kam piha veter in ali ima Nanos kapo. Za orientacijo glede datumov in dinamike prihoda front pa si je pomagal z dejstvom, da je tisto leto, ko na Pankracija ni mraza, na Zofko (se pravi kake tri dni kasneje) ponavadi dež.

Nekaj vremenskih pregovorov

Takšno napovedovanje vremena je temeljilo na dolgoletnih izkušnjah. Inteligentni ljudje so desetletja in desetletja zbirali podatke in sestavljali pravila. Seveda ne na papir, temveč so si jih zapomnili. Še moj oče je za mnoga leta vedel, na kateri dan je prvič zapadel sneg.

Seveda sklepanje iz opaženih primerov ni omejeno le na vreme. Na najrazličnejših področjih lahko zbiramo podatke, opazimo vzorce in sestavimo pravila, s katerimi lahko določamo neznane lastnosti v novih primerih.

Veja umetne inteligence, ki oponaša to veščino — kot pač umetna inteligenca že po definiciji oponaša človeško --, je strojno učenje (machine learning). Na podlagi podatkov, ki opisujejo določene lastnosti (attribute, feature, variable), poskušamo sestaviti napovedni model (prediction model), s katerim napovemo izid ali določimo neko lastnost, recimo vrsto objekta.

Kadar vedo, da bo dež, vremenoslovci vedežujejo?

Besedi napovedovanje in napovedni model sta nekoliko zavajajoči. Ne gre za napovedovanje stvari, ki se bo šele zgodile, temveč za predvidevanje, določanje neke lasnosti, ki je še ne poznamo. Da, vremenoslovci res napovedujejo vreme. A ko pridemo k zdravniku, ta na podlagi simptomov ugotovi, katera (upamo: nobena) bolezen nas daje. Tudi temu rečemo »napovedovanje«.

Računalniško sestavljeni napovedni modeli so povsod. Ne uporabljajo jih le vremenoslovci: banke imajo sisteme, ki prepoznajo sumljive transakcije in nabiralniki elektronske pošte prepoznavajo neželeno pošto, ponudniki mobilne telefonije poskušajo zaznati, katere stranke jim bodo ušle h konkurenci, razvijalce zdravil zanimajo učinki novih sestavin, avtomobili vedno natančneje prepoznavajo ovire na cesti … Napovedni modeli so že dolgo neopazni del našega vsakdana.

Sodobni napovedni modeli so zapleteni. Za sestavljanje globokih nevronskih mrež potrebujemo ogromno podatkov, zapletene algoritme, močne računalnike in ogromne pomnilnike, za njihovo uporabo pa neprimerno veliko energije. Preproste modele pa lahko sestavimo tudi v razredu.

Poglavje 2: Ozadje: Modeli

Bistvo te aktivnosti je predstaviti idejo napovednega modela. Model lahko sestavimo »na pamet« na podlagi znanja, ki ga imamo o nekem področju. Postopki strojnega učenja (machine learning) pa ga sestavijo na podlagi učnih primerov.

Model je zapisan v določeni formalni obliki. To, kar učenci najprej odkrijejo, so klasifikacijska pravila (odločitvena pravila, decision rules). Ko jih pripravimo do tega, da to prepišejo v obliko drevesa, dobimo klasifikacijsko ali odločitveno drevo (classification tree).

Klasifikacijsko drevo je sestavljeno iz notranjih vozlišč, v katerih se na podlagi določene lastnosti odločimo za eno od vej drevesa. Končne točke (računalnikarji temu rečemo listi drevesa) uvrstijo palčka (ali karsižebodi) v določeno skupino.

Drevesa so eden od prvih modelov, ki smo jih sestavljali s strojnim učenjem. Čeprav niso tako zmogljiva kot sodobni modeli, jih zaradi njihove preprostosti še vedno radi uporabljamo kot primer.

Model povzema bistvene lastnosti učnih podatkov. Za klasifikacijo prihodnjih primerov (novih palčkov, katerih vloge ne poznamo, a jo želimo napovedati) ne potrebujemo več učnih podatkov, temveč za to zadošča že model.

Strojno učenje posplošuje (generalization) posamične primere v splošna pravila. Več ko imamo primerov in bolj ko so le-ti pravilni, bolj zanesljiv je model.

Celo v četrtem razredu smo po zaključku takšne učne ure že razpravljali o tem, da bi lahko na podoben način sestavili model, ki bi povedal, ali je določeni učenki všeč določena šolska malica: zbrati bi morali dovolj različnih primerov malice, popisati njene lastnosti in si zapisati učenkino mnenje o njej. Učencem smo nato povedali, da se podobni, le bolj zapleteni modeli, uporabljajo tudi v resnici, saj lahko z njimi povemo, ali je nekdo zbolel za neko boleznijo (in katero), ali bo jutri lepo vreme in ali bo neko zdravilo delovalo ali ne.

Poglavje 3: Kaj počnejo palčki (z računalnikom)?

Kaj počnejo palčki je smiselno končati tako, da pokažemo model, ki ga zgradi računalnik, saj lahko na ta način nadaljujemo s pogovorom o tem, da se takšni (in bolj zapleteni) modeli uporabljajo tudi v praksi in za zaresne stvari.

Aktivnosti je zato priložen preprost delotok za program Orange. Ta je že nastavljen, tako da lahko v razredu le odpremo okna s podatki, drevesom in napovedmi. Tule pa ga bomo še dodatno razložili, da ga bomo boljše razumeli in znali po potrebi kaj spremeniti, popraviti ali dodati.

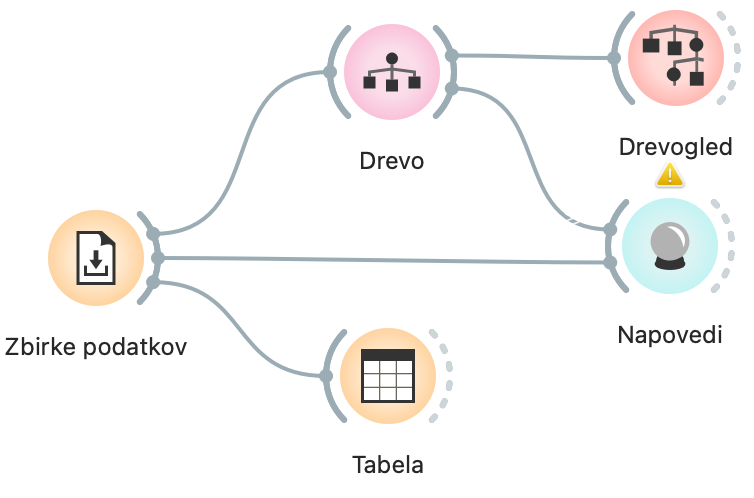
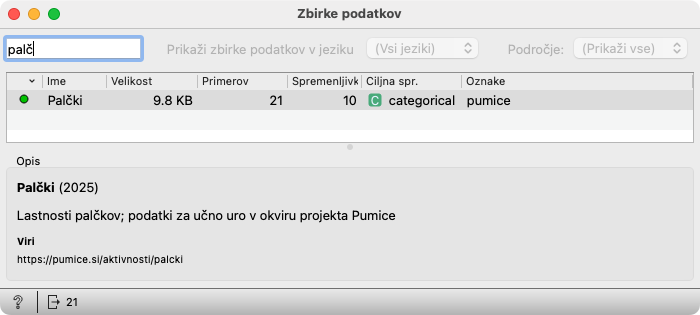
Zbirke podatkov je nastavljen tako, da prenese s spleta podatke o Palčkih. Če bi jih morali poiskati sami, bi v polje levo zgoraj natipkali začetek imena podatkovne zbirke (palč...). Ko se podatki pokažejo v spodnji tabeli, jih dvokliknemo.

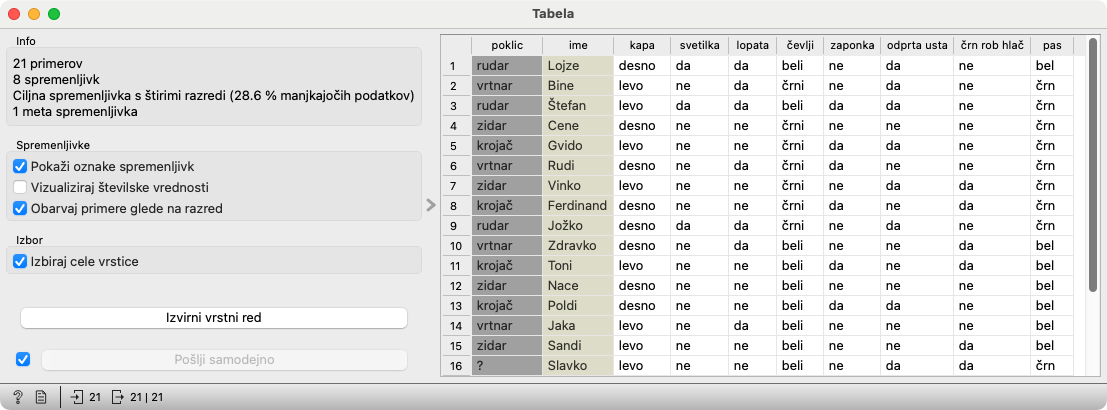
Na Zbirke podatkov je priključen gradnik Tabela. Z njim učencem pokažemo podatke, s katerimi bo delal računalnik. To je pomembno zato, da vidijo, da poleg pomembnih lastnosti dobi tudi nepomembne, kot so barva pasu, čevljev in oblika kape, ki pa jih bo računalnik prezrl kot nepomembne, tako kot so jih oni.

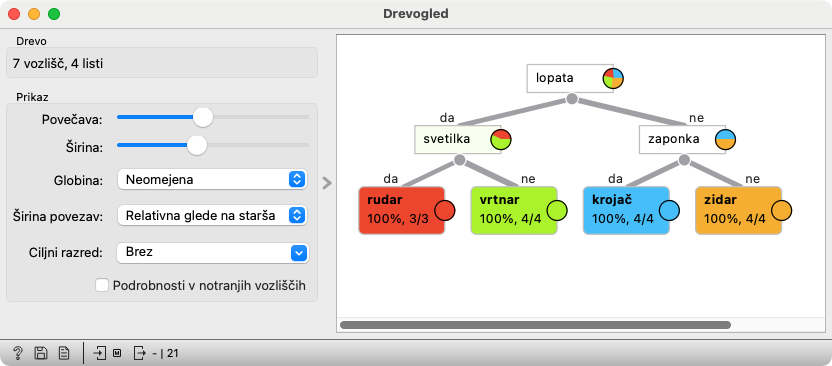
Na Zbirke podatkov je priključeno Drevo, ki sestavi drevo, in na Drevo Drevogled, ki to drevo pokaže. Nastavitve gradnika Drevo tu niso pomembne in ne bi smele vplivati na obliko drevesa.

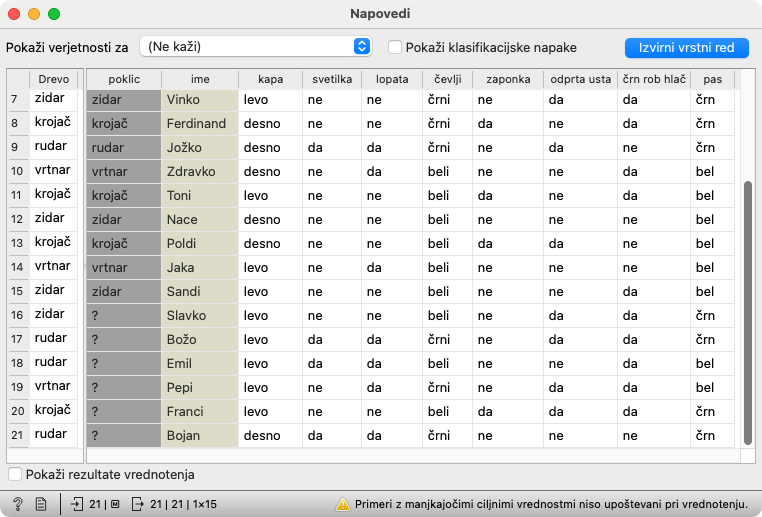
Gradnik Napovedi potrebuje podatke, za katere naj sestavlja napovedi (dobi jih iz Zbirke podatkov) in napovedni model (v našem primeru ga dobi iz Drevo). Gradnik kaže različne stvari, ki jih ne potrebujemo; v izogib moteči navlaki je v delotoku izključen prikaz verjetnosti in klasifikacijskih napak (zgoraj) ter rezultatov vrednotenja (med tabelama, oziroma na dnu, ko se spodnja tabela skrije).

Razširitev delotoka: odločitvena pravila

Morda bi učence (ali učitelja :) zanimalo, ali lahko računalnik poišče tudi pravila, kakršna so učenci sestavili v začetku, kot denimo »če ima zaponko in nima lopatke, je krojač.« Takšnim pravilom rečemo odločitvena pravila.

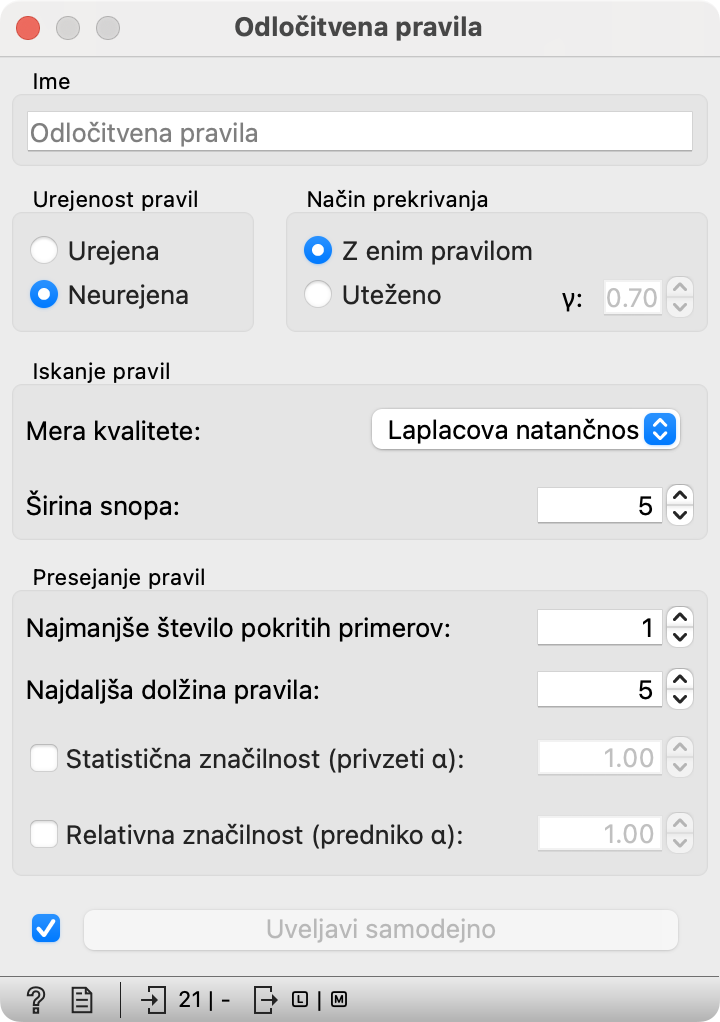
Na zbirke podatkov lahko pripnemo gradnik Odločitvena pravila in nanj Pregledovalnik pravil.

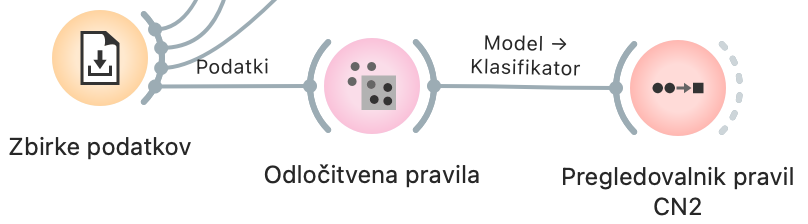
Pravila, kakršna so sestavljali učenci, bomo dobili, če zahtevamo kot mero kvalitete določimo »Laplacova natančnost«.

Poleg tega lahko preskusimo Urejena ali Neurejena pravila. Pri prvih je potrebno brati pravila eno za drugim; določeno pravilo uporabimo le, če za palčka ne velja nobeno od prejšnjih pravil. Pri neurejenih pravilih je vrstni red nepomemben. Katera je primernejša, je odvisno od tega, kako so svoja pravila izrazili učenci.

Pravila vidimo v Pregledovalnik pravil. Da bodo lepše izpisana, lahko vključimo Stisnjen pregled.

Poglavje 4: Prepoznavanje štirikotnikov

Prepoznavanje štirikotnikov lahko v celoti izvedemo na papir, na računalnik ali pa kombiniramo oboje. Tule opisujemo nekaj podrobnosti v zvezi z izvedbo na računalniku.

Uporaba spletne strani za vnos podatkov

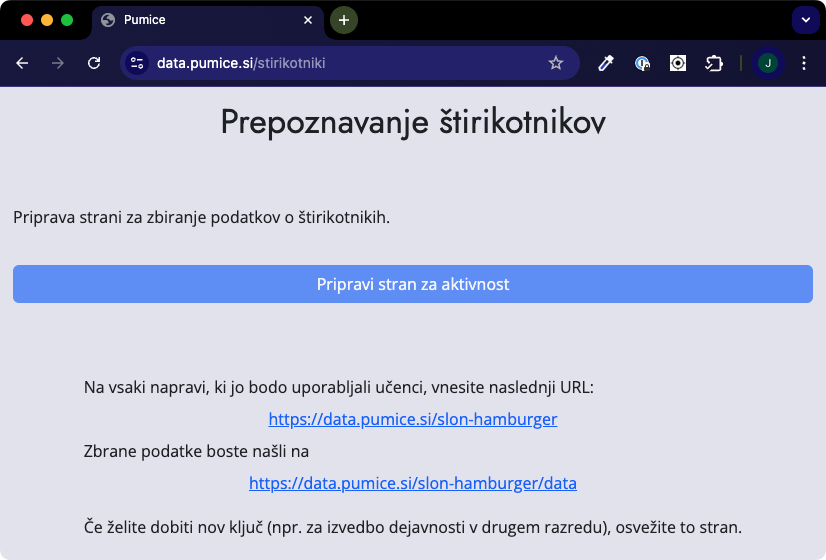
Obrazec za vnos podatkov pripravimo na strani https://data.pumice.si/stirikotniki. Pritisnemo »Pripravi stran za aktivnost«, pa dobimo dve povezavi: prvo vnesemo v tablice ali računalnike, ki jih bodo učenci uporabljali za vnos podatkov. Drugo bomo vnesli v Orange, da dobimo zbrane podatke.

Ure se lahko lotimo tako, da razredu razdelimo en komplet štirikotnikov. V tem primeru potrebujemo samo eno povezavo.

Če učence razdelimo v skupine in vsaka skupina dobi svoj komplet, se lahko odločimo, da bodo vse skupine vnašala podatke v skupno tabelo in se bo vsak lik pojavil večkrat (s čimer ni nič narobe — nasprotno, še lažje bo zaznati napake) ali pa naredimo ločeno tabelo za vsako skupino. To storimo tako, da osvežimo stran v brskalniku (F5 ali Ctrl-R oz. Cmd-R) in ponovno pritisnemo Pripravi stran za aktivnost.

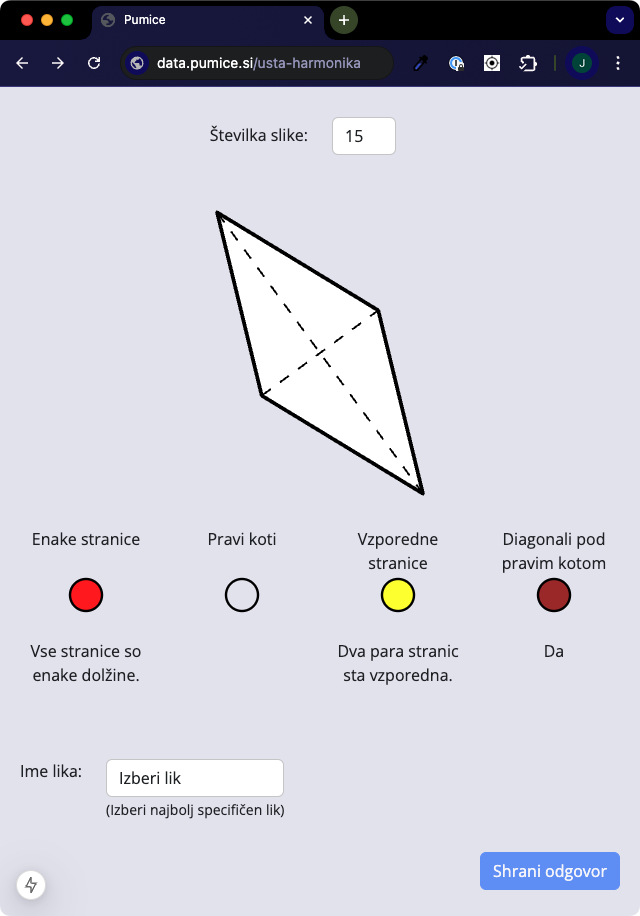
Učence bo na povezavi pričakal obrazec, podoben karticam. Ko vpišejo številko lika, dobijo sliko like, kroge za označevanje lastnosti in izbirnik oblik.

Kroge »barvajo« s klikanjem. Če kliknejo na krog večkrat, se barva spremeni; prvi krog se po prvem kliku obarva rdeče, po drugem modro, po tretjem je spet prazen. Podobno se vede tretji krog. (Brez skrbi, učenci se bodo že znašli. :)

Vsakemu liku morajo določiti tudi obliko, nato pa oddajo odgovor in nadaljujejo z naslednji likom.

Delotok

Delotok za Orange je kar velik, vendar je (skoraj) vse prednastavljeno, tako da nima kaj iti narobe. Za vsak slučaj povejmo, kaj se dogaja v posameznem gradniku in na kaj moramo popaziti.

Osrednja gradnika sta Drevogled in Napovedi. S prvim opazujemo sestavljeni model, drevo, in z drugim pregledujemo njegove napovedi. Oba očitno potrebujeta drevo, ki smo ga sestavili; dobita ga iz gradnika Drevo.

Zdaj pa poglejmo začetek: tam sta dva gradnika Datoteka. Gornji naloži primere štirikotnikov, ki jih uporabljamo za gradnjo drevesa - zato je povezan z Drevo. Spodnji naloži testne primere, zato je povezan z Napovedi.

Poleg tega imamo še tri gradnike, namenjene opazovanju. Prvi Tabela je povezan z vhodnimi podatki. Tam je zato, da lahko učencem pokažemo, da se računalnik uči (torej: da računalnik sestavlja drevo) iz enakih podatkov, kot so ga oni. Drugi gradnik Tabela in gradnik Pregledovalnik slik sta priključena na Drevogled. Če klikamo po delih drevesa, bosta tadva gradnika pokazala pripadajoče like. To uporabljamo v dva namena. Najprej zato, da pokažemo, kako računalnik deli like na enak način, kot so učenci delili kartice na mizi. Kasneje, ko se učimo iz podatkov, ki so jih zbrali učenci, pa uporabljamo to Tabelo in Pregledovalnik slik za iskanje napak v podatkih.

Datoteka

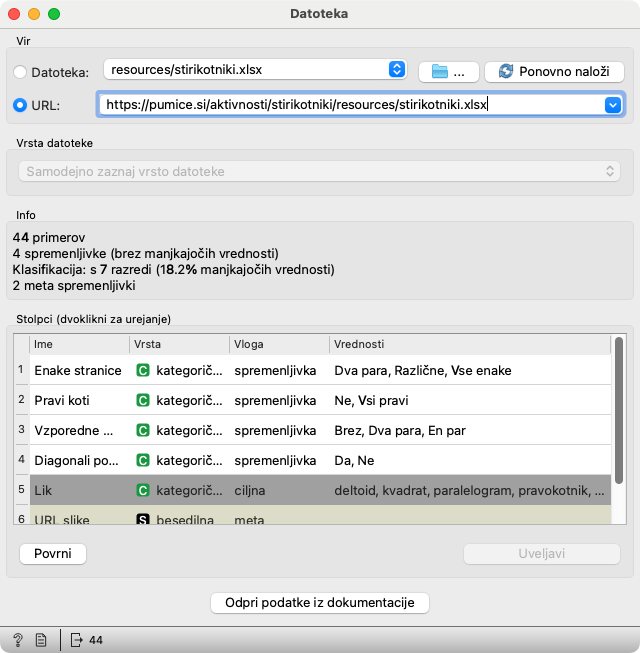
Oba gradnika Datoteka sta prednastavljena tako, da bereta podatke s spletne strani. V obeh mora biti izbran URL; prvi mora kazati na https://pumice.si/stirikotniki/resources/stirikotniki.xlsx in drugi na https://pumice.si/stirikotniki/resources/stirikotniki-testni.xlsx. Če zaradi spremembe spletne strani povezave ne bi več delovale (in bi pozabili popraviti delotok in tale dokument, za kar se že vnaprej opravičujemo :), jih poiščite v okvirčku na vrhu opisa aktivnosti.

Za učenje iz podatkov učencev, zamenjamo URL z URLjem, ki smo ga dobili na strani za vnos podatkov. Gradnik si zapomni nekaj zadnjih povezav: če se želimo, recimo, vrniti na izvirne podatke ali pa preklapljati med podatki, ki so jih zbrale različne skupine, pritisnemo na puščico desno od polja za vnos URL.

Drevo

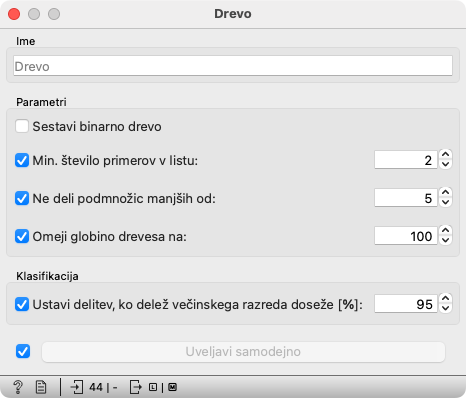
V gradniku za sestavljanje drevesa, Drevo, je več nastavitev. Za nas je pomembna le prva, Sestavi binarno drevo. Če je vključena, bo algoritem sestavil drevo, v ki ima v vsakem vozlišču le dve veji. Pri lastnostih z več možnimi vrednostmi, bo nekatere združil. Tako lahko, recimo, po kriteriju »Enako dolge stranice« da na eno stran »Vse«, na drugo pa preostali možnosti, torej »Dva para« ali »Brez«.

Takšna, binarna drevesa, imajo teoretične in praktične prednosti. V učni uri pa s tem ne opletamo. Učenci sestavljajo drevesa, ki imajo lahko tudi po tri veje, zato je »Sestavi binarno drevo« boljše izključiti.

Ostale izbire vplivajo na vedenje algoritma v primeru napak v podatkih. Če imamo v neki skupini 50 rombov in 5 kvadratov, so kvadrati verjetno narobe označeni, zato jih je smiselno zanemariti. V uri s štirikotniki, nimamo tako veliko likov, napake pa bomo opazili ne glede na te nastavitve.

Drevogled

O Drevogledu moramo vedeti predvsem, da lahko klikamo na posamezna vozlišča drevesa, pa bo gradnik posredoval pripadajoče like gradnikom, povezanim nanj — v našem primeru Pregledovalniku slik in Tabeli.

Pod vsakim notranjim vozliščem drevesa je krog, iz katerega izhajajo veje. Če kliknemo na ta krog, skrijemo (in s ponovnim klikom pokažemo) del drevesa, ki sledi temu vozlišču. To je lahko uporabno, če je potrebno razlagati postopek sestavljanja drevesa.

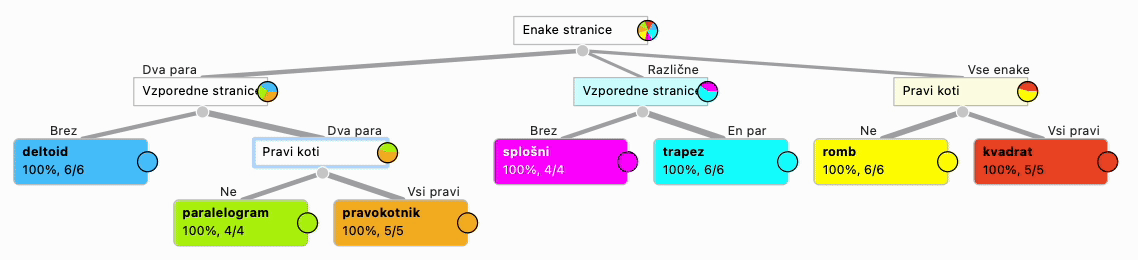
Na levi strani lahko zmanjšamo in zožamo drevo. Manjšamo tam, kjer piše Povečava in ožamo, kjer piše Širina. Tako pač je. :)

Pregledovalnik slik

Pregledovalnik slik ima dve pomembni nastavitvi.

Prva določa ime stolpca v podatkih, ki vsebuje URLje slik. V pripravljenem delotoku je vrednost je že nastavljena. Če gre kaj narobe, jo poskuša uganiti, tako da pogleda vsebine stolpcev. Če zgreši, ju pač nastavimo ročno: pravilna izbira je »URL slike«.

Druga vsebuje ime stolpca z besedilom, ki ga bo pokazal pod vsako sliko. Ko delamo s podatki, ki so jih vnesli učenci, so v stolpcu Lik zapisani njihove izbire, v Pravi lik pa pravilne oblike likov. Ko delamo z vnaprej pripravljenimi podatki, bosta oba stolpca enaka.

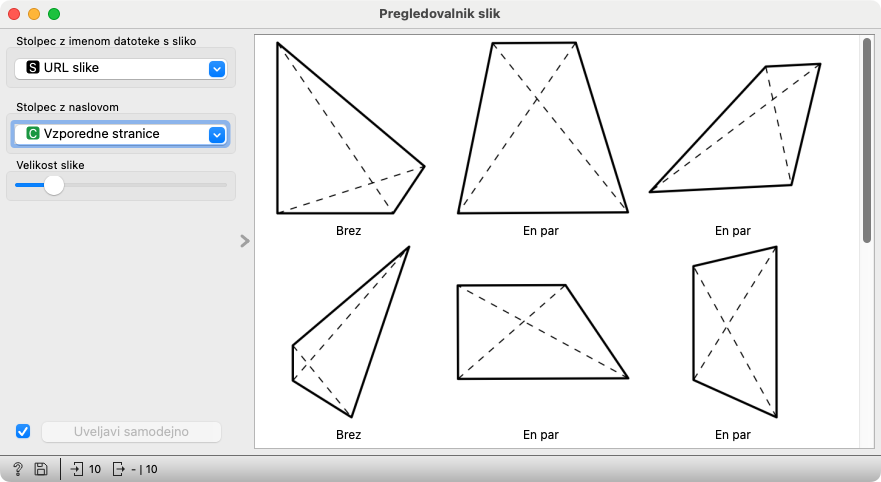
Nihče nas ne bo kregal — niti grdo gledal — če namesto oblike izberemo katero od lastnosti. Nasprotno: na ta način najlažje poiščemo morebitne napačno določene lastnosti. Če ima lik na sliki dva para vzporednih stranic, pod njim ne bi smelo pisati, da je brez njih.

Poglavje 5: Živalsko drevo

Čeprav v uri Živalsko drevo stalno uporabljamo Orange, se tudi manj izkušenemu učitelju ni česa bati, saj je vse že pripravljeno. Edino, česar ne smemo pozabiti, je, da po vsaki spremembi preglednice v Excelu le-to shranimo, v Orangeu pa jo ponovno naložimo.

Preglednica v Excelu ima dve skriti vrstici. Kaže ju pustiti takšni, kot sta. Da ne bi česa zamolčali, pa tule povejmo, kaj se skriva v njima.

• Vrstica 2 definira tip podatkov v stolpcu. V njej piše, da so v prvem stolpcu zgolj imena živali, in se ta stolpec zato ne sme pojaviti kot kriterij v drevesu.
• Vrstica 3 pove vlogo stolpca. V njej piše, da vsebuje drugi stolpec tisto, kar želimo napovedati. Če tega ne bi bilo, bi Orange lahko mislil, da želimo na podlagi tega, ali za katero skupino živali gre, napovedati, ali zna leteti. (V resnici ne bi: pritožil bi se, da ne ve, kaj želimo od njega.)

Poglavje 6: Algoritem za sestavljanje drevesa

Drevesa sestavljamo s preprostim rekurzivnim algoritmom

če so izpolnjeni pogoji za konec
  vrni list
sicer
  poišči najboljši kriterij za delitev primerov
  če ni primernega kriterija
    vrni list
  razdeli primere na podmnožice
  rekurzivno sestavi drevo za vsako podmnožico
  vrni vozlišče z najboljšim kriterijem in poddrevesi

Pri sestavljanju drevesa za določanje poklica palčkov in še bolj pri drevesu za določanje oblike štirikotnikov, smo izvajali prav ta algoritem. Pogoj, da določene množice nismo delili naprej, je bil, da so imeli vsi palčki enak poklic ali vsi štirikotniki pripadali isti vrsti štirikotnikov. Primeren kriterij … je bil pač kriterij, ki lepo deli množico v podmnožice.

Za splošni algoritem bo potrebno te pogoje in kriterije definirati formalno.

Najprimernejši kriterij

Intuicija je čisto preprosta: najprimernejši kriterij je takšen, ki deli učne primere tako, da pridejo na eno stran primeri enega, na drugo stran primeri drugega razreda. Če je razredov (torej poklicev ali oblik štirikotnikov) več, si pač želimo takšnega, pri katerem se ne bo dogajalo, da bi se primeri iz istega razreda pojavljali v več podmnožicah.

Če se temu da izogniti.

V praksi moramo namreč računati s tem, da lastnosti morda ne zadoščajo za popolno ločitev primerov. Morda se tega ne da v principu, saj je razred delno odvisen od naključja. Včasih pač nimamo vseh potrebnih lastnosti. Še pogosteje so v lastnostih ali pa v razvrstitvi napake. Kriterij, ki smo si ga zamislili zgoraj, je v praksi preoptimističen.

Želimo si čim manjša drevesa. Razlogov za to je kup.

• Manjša drevesa je lažje razumeti. Razumevanje modelov je pomembno.
• Z merjenjem lastnosti so lahko povezani stroški. Želimo si, da bi vsaka odločitev zahtevala čim manj meritev, čim manj lastnosti.
• Pri gradnji dreves drobimo podatke na vedno manjše podmnožice. Lahko nam jih zmanjka. Če začnemo gradnjo z neko nesmiselno, neinformativno lastnostjo, smo brez potrebe razpolovili podatke. Na levi in desni strani bomo morali sestaviti v načelu enaki drevesi, a s polovico manjšo množico učnih primerov.
• Končno, po načelu Ockhamove britve med več razlagami istega pojava bolj zaupamo preprostejši.

Iskanje drevesa, ki bi bilo najkrajše in dalo minimalno napako je NP-poln problem. To pomeni, da ni znanega algoritma, ki bi ga reševal v doglednem, polinomskem času.

Izbor kriterijev mora biti torej takšen, da vodi v čim krajša drevesa. Postopek izbora je hevrističen: za vsako lastnost izračunamo določeno mero, ki nam pove, kako dobra je videti. Izberemo tisto, ki je videti najboljša. Mera ne vodi nujno v najkrajša možna drevesa (recimo: najkrajša možna med vsemi drevesi, ki karseda pravilno razvrstijo učne primere), vendar v večini primerov vodi v kar dobra drevesa.

Ideja večine mer je, da ocenjujejo nečistočo množice primerov. Ogledali si bomo dve preprosti.

Prva je Ginijev indeks. Ta pravi, da je nečistoča množice enaka verjetnosti, da bosta dva naključno izbrana elementa množice pripadala različnima razredoma.

Recimo, da imamo $n$ primerov, od katerih jih $n_i$ pripada $i$-temu. Verjetnost, da naključno izbrani primer pripada $i$-temu razredu, je potem $p_i = n_i / n$. Ginijev indeks je potem

$G = \sum_i p_i(1 - p_i).$

Gremo čez vse razrede. Če izberemo dve primera, je $p_i$ verjetnost, da bo prvi v $i$-tem razredu in $1 - p_i$ je verjetnost, da bo drugi v nekem drugem razredu. Formulo lahko še malo poenostavimo:

$\sum_i p_i(1 - p_i) = \sum_i (p_i - p_i^2) = \sum_i p_i - \sum_i p_i^2 = 1 - \sum_i p_i^2,$

pa imamo

$G = 1 - \sum_i p_i^2.$

Druga, še popularnejša mera nečistoče je entropija. Ta je definirana kot

$H = -\sum_i p_i \log_2 p_i.$

Če bi spraševali za vsak primer posebej, bi to v vsakem primeru zahtevalo 1 bit informacije. V drugem primeru, ko je v enem razredu, na primer, natančno en primer od stotih, pa lahko shajamo s sedmimi vprašanji. Prvo se glasi: je oni posebni primer med prvimi petdesetimi. Drugo bo: je med prvimi 25 ali med 51. in 75. Kako gre naprej, je že jasno, ne? Tako bomo s samo 7 vprašanji izvedeli razred vseh primerov. V poprečju je to 7/100 = 0.07 vprašanj na primer. Entropija, $-(0.01\log_2 0.01 + 0.99 \log_2 0.99) = 0.08$, kar je kar blizu; razlika izhaja iz … no, iz poenostavljanj. :)

Ta je kar lepo razložena na slovenski Wikipediji. Entropija meri količino informacije, ki jo potrebujemo, da izvemo rezultat nekega izida. Če imamo dva razreda in je v vsakem od njiju po 50 primerov, je entropija enaka $-(1/2 \log_2 1/2 + 1/2 log_2 1/2) = 1$. Da izvemo, v kateri razred sodi naključno izbrani primer, potrebujemo 1 bit informacije, eno vprašanje z binarnim odgovorom. Če je v enem razredu 99 primerov in v drugem en, je entropija skoraj 0. Da izvemo, v kateri razred sodi naključno izbrani primer, potrebujemo skoraj nič informacije.

Poleg teh dveh obstaja še kup drugih mer nečistoče.

Kako uporabimo mere nečistoče za izbor lastnosti? Takole.

• za vsako lastnost pogledamo podmnožice, v katere nam razdeli učne primere.
• Za vsako podmnožico izračunamo njeno nečistočo.
• Izračunamo uteženo povprečje nečistoč: utežimo jih z velikostjo podmnožic.

Tako dobimo *pričakovano nečistočo po uporabi te lastnosti.

Izberemo lastnost, ki nam da največje (pričakovano) zmanjšanje nečistoče.

Kriteriji za konec gradnje

V algoritmu se pojavijo na dveh mestih: prvi je na začetku, »če so izpolnjeni pogoji za konec«, drugi je pred rekurzivnim klicem, »če ni primernega kriterija«.

Kakšni bi bili pogoji za konec? Očiten pogoj je, da so vsi primeri že v istem razredu. V praksi se zadovoljimo tudi, če je večina v istem razredu večina primerov. 95% je že kar dovolj.

Drugi pogoj je, da nam primerov zmanjkuje. Pri razlikovanju štirikotnikov imamo lastnosti v več kot dvema možnostima: število parov vzporednih stranic je lahko 0, 1 ali 2. Če uporabimo tako lastnost, vendar se izkaže, da, na primer, ni primerov s po dvema vzporednima stranicama, ni česa deliti. (Res pa imamo v tem primeru tudi težave z listom, ki ga bomo vrnili). V praksi prekinemo gradnjo, ko je primerov, recimo, manj kot 5.

Kakšni pa bi bili kriteriji za »primerno lastnost«? Če neka lastnost ne zmanjša nečistoče, je očitno neuporabna. Če ni nobene, ki bi jo zmanjšala, smo zaključili. Lahko se zgodi tudi, da smo uporabili že vse lastnosti (kar se v bistvu prevede na prejšnji stavek).

Izogibamo se tudi listov s premalo primeri. Popularen kriterij je, da nikoli ne uporabimo lastnosti, pri kateri bi imela neka podmnožica manj kot določeno število primerov. (Tradicionalen prag je kar 2.)

Listi

Listi drevesa vsebujejo informacijo o razredu, v katerega spadajo primeri. Včasih je to en sam razred (vsi palčki z lopatko, a brez lučke, so vrtnarji), včasih pa je to verjetnost razredov (med osebami, mlajših od 50, ki dosežejo srčni utrip vsaj 150, jih ima le 10 % zamašene srčne arterije).