Priporočilni sistemi

Poglavje 1: O priporočilnih sistemih

Zanimivo dejstvo: GPS mora upoštevati relativnostno teorijo. Ker so sateliti dalj od središča Zemlje kot sprejemniki, je tam gravitacija nižja in njihove ure tečejo hitreje. Razlika je +45.8 μs na dan! Čeprav signali potujejo s svetlobno hitrostjo, v času, ki bi ga povzročila napaka enega samega dneva, prepotujejo že dober meter.

Ko je napisal, da je »vsaka dovolj napredna tehnologija neločljiva od magije,« je imel Arthur C. Clarke bržkone prav. Če si le ni predstavljal, da nas bo ta magija kaj pretirano čudila, pretresala ali celo strašila, saj bi se v tem primeru — motil. Vsako dovolj razširjeno tehnologijo hitro vzamemo za samoumevno. Ko postane del življenja, nikogar ne zanima, ali se za njo skrivajo polprevodniki ali magični uroki. Da telefon na nekaj metrov natančno ve, kje smo (in to celo stalno deli z našimi bližnjimi), nikogar ne čudi, čeprav o delovanju te tehnologije (ali magije?) običajni Zemljan — in tudi večina neobičajnih — ne ve dosti več kot o delovanju urokov iz Harryja Potterja.

Ena od tehnologij, ki je zaradi svoje razširjenosti postala neopazna, so priporočilni sistemi. V glasbenih aplikacijah in na straneh z video posnetki nam kažejo pesmi in posnetke, ki nam bodo morda všeč; v trgovinah nam ponujajo izdelke, ki jih bomo morda kupili; na spletnih straneh za načrtovanje izletov nam svetujejo nove poti, podobne tistim, po katerih smo hodili, tekali in kolesarili doslej; in na družabnih omrežjih nam menda najdejo nove prijatelje.

Priporočilni sistemi usmerjajo naše življenje. Za takšne reči je najbrž koristno vedeti, kako delujejo. Hkrati pa je njihovo delovanje dovolj preprosto (in zanimivo!), da ga lahko razložimo že četrtošolcem. Ne le razložimo, temveč brez težav (in brez računalnika) uprizorimo sami.

Priporočilni sistemi za razliko GPS niso ravno znanost: kaj morajo početi in kako to doseči, je očitno. Če se zanimamo za nakup novega zadnjega menjalnika za kolo, nam morajo ponuditi še prednji menjalnik, verigo in zobnike.

V letu 2024 so na YouTube vsako minuto naložili za 500 ur novih posnetkov. Kako naj se YouTube odloči, komu jih ponuditi v ogled?

Povezave med izdelki — kaj ponuditi ob čem — je potrebno seveda razbrati iz podatkov. Ročno vnašanje bi bilo zamudno, manj natančno in pogosto tudi nemogoče. Priporočilni sistemi temeljijo na opazovanju podobnosti. Dva izdelka, videa, sliki, pesmi … sta si podobna, če zanimata iste ljudi. Če so Ana, Berta in Cilka poleg Taylor Swift poslušale še Duo Lipo, sta si pevki najbrž podobni, vsaj slogovno. (Avtor pričujočega besedila za to sicer ni strokovnjak). Ko bo Dani poslušala eno od njiju, ji bo torej smiselno priporočiti še drugo.

Resnični priporočilni sistemi delajo tako tole kot zgornje in še kaj zraven.

Gremo pa lahko tudi v nasprotno smer. Namesto, da izmerimo podobnosti med glasbeniki (češ, dva glasbenika sta si podobna, če ju poslušajo isti ljudje) ter vsakemu slušatelju Taylor Swift priporočimo še vse njene podobnice, lahko izmerimo podobnosti med uporabniki. Dva kupca, dva gledalca video posnetkov ali dva načrtovalca nedeljskih izletov sta si podobna, če kupujeta, gledata in izbirata iste izdelke, posnetke in izlete. Če je potrebno narediti priporočilo za Jožeta in bomo ugotovili, da sta mu podobna Benjamin in Tone, mu bomo priporočili tisto, kar je bilo všeč njima.

Tule bomo gremo po drugi poti, saj je za izvedbo v razredu zanimivejša: učenci bodo izmerili podobnost svojih okusov za glasbo, risanke, filme, knjige ali karkoli že in si na podlagi tega oblikovali priporočila.

Poglavje 2: Spletna stran za vnos podatkov

Po tem, ko učenci izberejo svoje najljubše risanke, narišejo »okusogram« in iz njega razberejo priporočila, je uro smiselno nadaljevati tako, da s tablicami ali računalniki vnesejo svoje izbore na spletno stran, tako da lahko pokažemo priporočilni sistem iz podatkov za ves razred.

Za to pred uro pripravimo obrazec za vnos podatkov. Najprej izberemo vrsto podatkov: risanke, televizijske serije, glasbene skupine, lastne podatke ali podatke iz preteklega dogodba. Prvi in drugi so že pripravljeni. O lastnih podatkih bomo pisali spodaj. Če želimo ponoviti uro s podatki, ki smo jih naložili v preteklosti, pa izberemo četrto možnost in vpišemo ključ. Če je bil URL preteklega dogodka https://data.pumice.si/primer-opica, tu vpišemo primer-opica.

Določimo lahko še, koliko najmanj stvari bodo morali in koliko največ stvari bodo smeli izbrati učenci. Trenutna nastavitev, 7, je primerna za skupine z 8-10 člani, ki izbirajo med 50-70 rečmi. Ker so to tudi sicer smiselne velikosti skupin in števila reči, je ta nastavitev najbrž kar primerna.

Aktivnost smo poskušali z različnim številom reči, med katerimi izbiramo. Zdi se, da je primerna velikost izbora enaka številu reči, deljenemu z deset. Čez palec.

Gre za to, da morajo imeti dovolj izbire (da ne bodo izbrali vsi istih stvari, temveč se bodo »profilirali«), obenem pa ne preveč, da se ne bodo tako razpršili, da bo premalo skupnih izborov. Večje število reči, ki so na izbiro, poveča razpršenost. Večje zahtevano število izbranih reči očitno poveča preseke; če morajo izbrati preveč stvari, pa lahko njihovi izbori sovpadajo preveč, poleg tega pa to lahko postane naporno.

Če jih ne omejimo na natančno določeno število stvari, se zaplete izračun podobnosti. To opisujemo v naslednjem razdelku

Možnost »Premešaj vrstni red stvari« uporabimo, če ne bomo uporabljali kartic, temveč bodo učenci izbirali stvari neposredno s spletne strani. V tem primeru je namreč smiselno vsakemu učencu pokazati drugačen vrstni red.

Ko pritisnemo Pripravi stran za aktivnost, dobimo povezavo za vnos podatkov, ki jo vpišemo v tablice ali računalnike, ki jih bodo uporabljali učenci, in povezavo za prenos zbranih podatkov, ki jo vnesemo v Orangov delotok. Če kliknemo slednjo povezavo kar v brskalniku, pa si bomo prenesli Excelovo datoteko s podatki o izboru — seveda po tem, ko bodo učenci vnesli svoje izbore.

Poleg tega lahko tu dobimo PDF s karticami.

Priprava lastnih podatkov

Če želimo naložiti lastne podatke, jih pripravimo v Excelu. Možni sta dve obliki.

Pripravimo lahko tabelo z dvema stolpcema. V prvem so povezave na slike (na primer posterji risank), v drugem imena (naslovi risank), ki bodo izpisana pod karticami. Ogledate si lahko primer datoteke s serijami.

Druga možnost je tabela z več stolpci. Vsebina prvih dveh je takšna, kot opisujemo zgoraj, v ostalih pa so lahko poljubni dodatni podatki. V prvi vrstici tabele morajo biti imena stolpcev. Spletna stran ne bo uporabljala podatkov iz dodatnih stolpcev, pač pa bodo ti stolpci v tabeli s podatki o tem, kateri učenec je izbral katero reč. Naprednejši uporabniki Oranga lahko to uporabijo za bolj poglobljeno analizo, ki pa je tule ne bomo opisovali.

Če naložimo svoje podatke, bo spletna stran pripravili tudi PDF s karticami. Da bodo te lepše, je dobro, da imajo slike podobno (po možnosti: enako) razmerje med višino in širino. Če bodo nekatere slike pokončne, druge ležeče, bo na karticah z ležečimi slikami veliko praznega prostora.

Stran, ki jo uporabljajo učenci

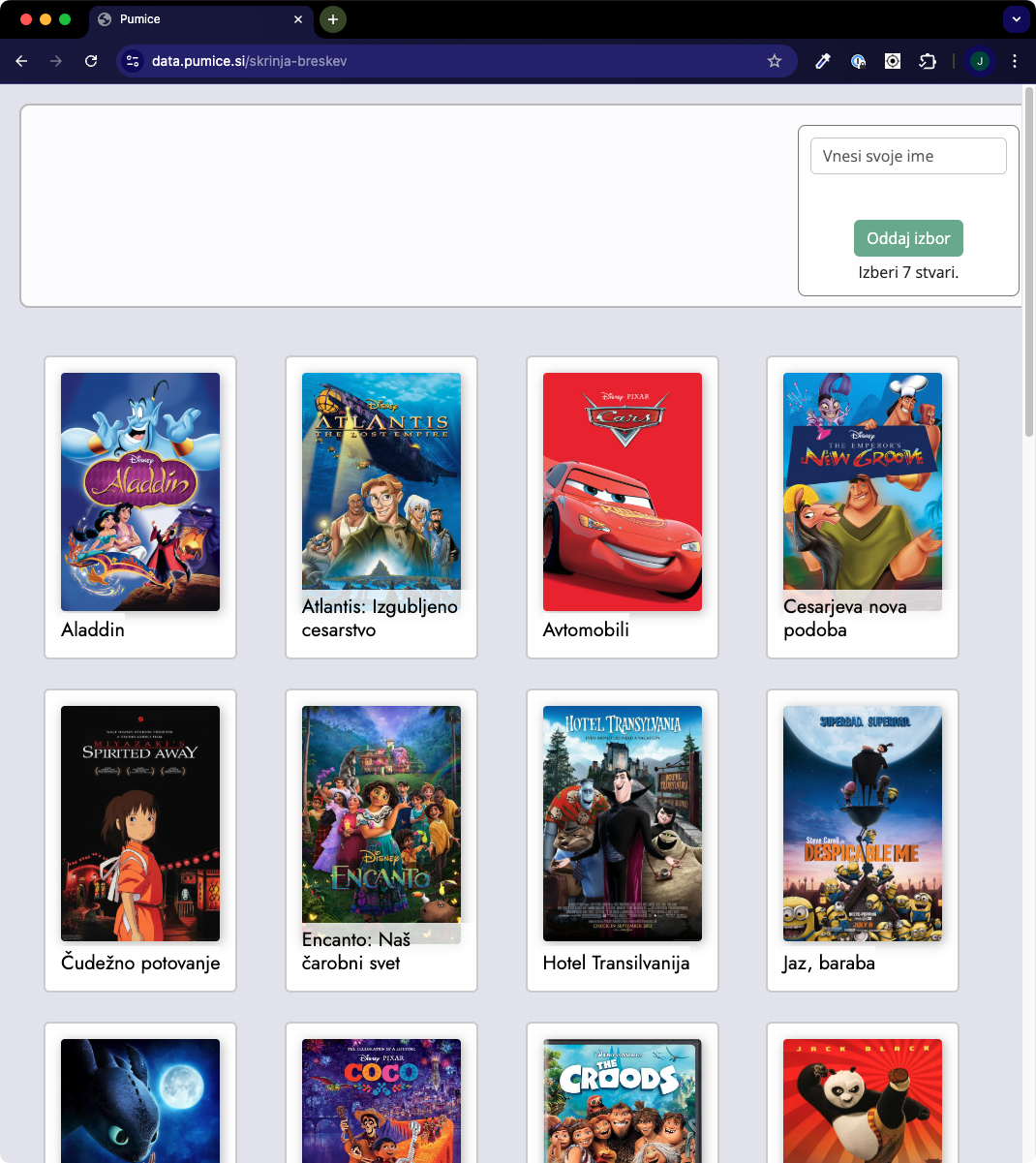
Na povezavi, ko jo dobimo na strani za pripravo obrazca, na primer https://data.pumice.si/skrinja-breskev je stran, na kateri učenci izbirajo risanke, serije, glasbenike oz. druge stvari. Ko izberejo ustrezno število stvari in vpišejo svoje ime (sistem pazi, da dva učenca ne bi vpisala enakega imena, zato morajo po potrebi dodajati prvo črko priimka) lahko oddajo izbor in predajo tablico naslednjemu učencu.

Stran trenutno ni primerna za uporabo na manjših zaslonih, recimo telefonih.

Poglavje 3: Več o izvedbi z računalnikom

Računalnik za učno uro ni potreben. Po izkušnjah je učencem tudi ta del sicer zanimiv, učitelj pa naj sam presodi, ali ga izvesti ali ne.

Učitelji, ki se ne želijo poglabljati v to, kako je sestavljen delotok za Orange, ki ga bodo uporabili v razredu, bodo tale razdelek brez škode preskočili. S seboj povabim druge vas junake.

Če se odločimo za izvedbo z računalnikom, pred uro pripravimo povezavo za vnos podatkov, tako da na spletni strani izberemo že pripravljene podatke (Risanke, TV serije ali Glasbene skupine) ali pa naložimo svoje podatke, kot smo opisali v prejšnjem razdelku.

Na računalnikih s slovenskim operacijskim sistemom bi moral biti Orange privzeto nastavljen na slovenski jezik. Če ni, izberemo jezik v nastavitvah programa.

Za delo z računalnikom si je potrebno namestiti program Orange ter dodatka Networks in Pumice. Ta namestimo tako, da ju izberemo v Nastavitve / Dodatki, potrdimo izbor in ponovno zaženemo Orange.

Posebnega znanja uporabe Oranga ne potrebujemo, saj je na spletni strani Pumic objavljen že vnaprej pripravljen delotok za Orange. Vanj vnesemo povezavo za prenos zbranih podatkov in že lahko opazujemo »okusogram« za ves razred in priporočila za vsakega učenca.

Razumevanje delovanja delotoka ni potrebno, je pa koristno, zato v tem gradivu opisujemo njegove sestavne dele.

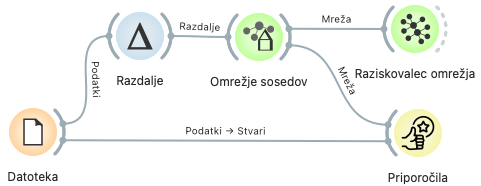
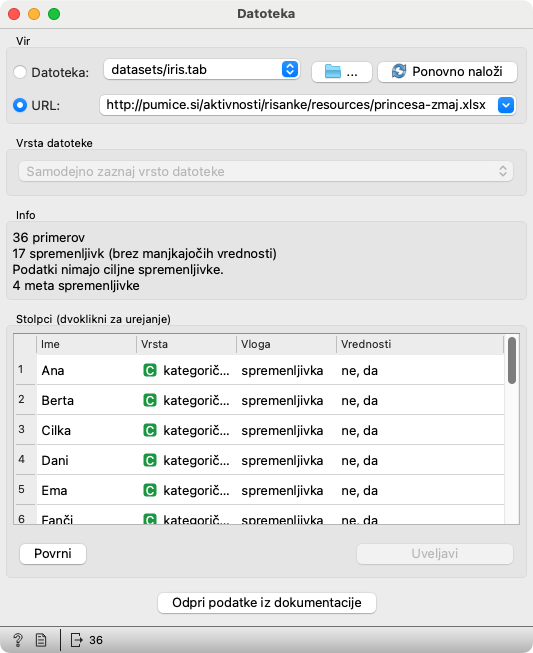
Gradnik Datoteka prenese zbrane podatke. V polje URL vnesemo povezavo na stran za prenos podatkov, ki smo jih zbrali v razredu. Če je bil URL za zbiranje podatkov, ki smo ga vpisali v tablice, https://data.pumice.si/princesa-zmaj, bodo podatki na https://data.pumice.si/princesa-zmaj/data. Privzeti URL prebere testne podatke.

Gradnik Razdalje izračuna razlike med učenci. Razdalja, ki jo uporabljamo, temelji na Jaccardovi podobnosti. Ta deli velikost preseka izborov z velikostjo njune unije. Čeprav učenci upoštevajo le preseke, bo vrstni red po podobnosti enak, ker vsak učenec izbere enako število objektov.

Tu ni česa spreminjati. Nekatere druge razdalje bodo dale smiselne rezultate, vendar je za naše namene najprimernejša Jaccardova, predvsem pa da rezultate enake postopku, ki ga uporabljajo učenci.

Sledi Omrežje sosedov. Vhod v ta gradnik je matrika razdalj. Iz tega sestavi mrežo tako, da vsakega učenca poveže s tremi najpodobnejšimi.

Gradnik lahko za vsak slučaj odprete in preverite, da je število sosedov nastavljeno na (privzeto) vrednost 3.

Lahko se igramo in spremenimo število sosedov na več ali manj in tako dobimo bolj ali manj splošna priporočila. Ena skrajnost, je, da so vsi sosedje z vsemi: tedaj bomo vsakemu priporočili to, kar je v razredu najpopularnejše. Druga je, da ima vsak le enega soseda: tedaj bo dobil priporočila le na osnovi enega sošolca ali sošolke.

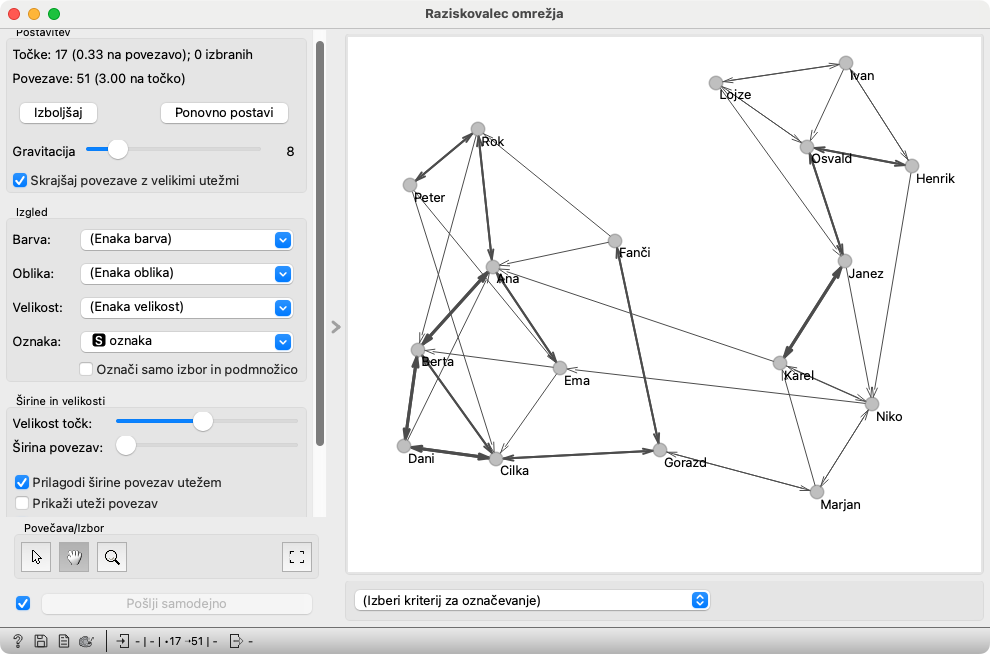
Podobnosti med učenci nam pokaže Raziskovalec omrežja. Povezave so usmerjene: od vsakega učenca vodijo natančno tri puščice. Včasih se zdi, da od koga vodita le dve: to se zgodi, če se črte prekrivajo.

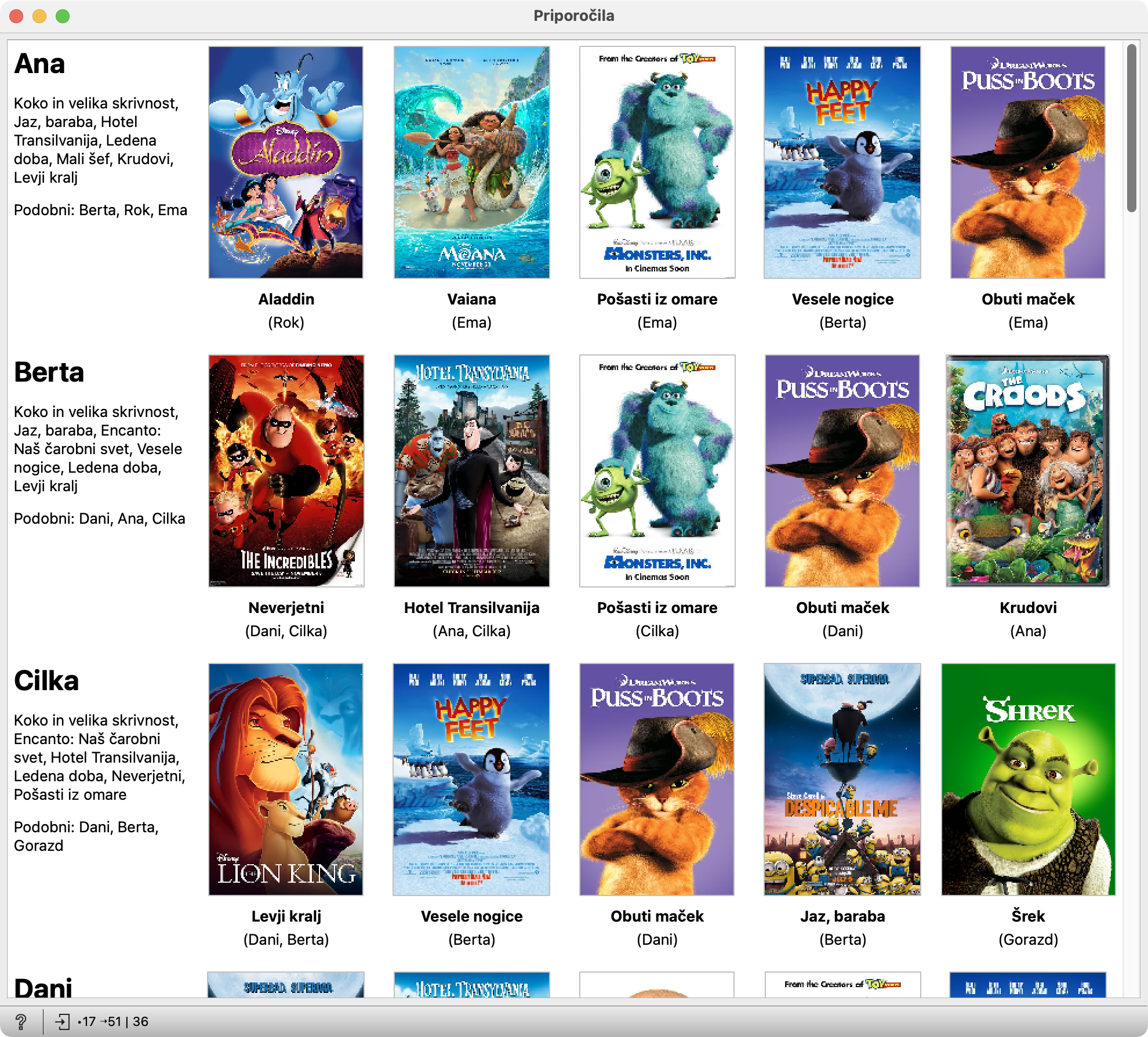
Gradnik Priporočila potrebuje mrežo podobnosti, ki jo dobi iz Omrežje sosedov, ter podatke o risankah, ki jih dobi iz Datoteka, zato ju je potrebno povezati z obema. Podatke o risankah potrebuje zato, da lahko izpiše njihove naslove in pokaže slike; mrežo potrebuje, da izračuna priporočila.

Poglavje 4: Več ozadja

Priporočilni sistem, ki smo ga sestavili v razredu, je seveda zelo poenostavljen. Za konec je tule poglavje za učitelje, ki bi se želeli bolj podkovati.

Grafi

Za graf prijateljstev so značilni trikotniki: osebi s skupnim znancem se najbrž poznata. Nasprotno pa so za mrežo sovraštev značilni štirikotniki: osebi s skupnim sovražnikom se ne sovražita, kaj verjetno pa imata še kakega drugega skupnega sovražnika. Tako dobimo štirikotnik sovražnikov.

Podobnosti smo predstavili v obliki grafa. Graf seveda ni nujno vedno narisan. Facebook in Twitter prav gotovo ne natisneta grafa prijateljev in sledilcev, saj bi bil prevelik (tri milijarde ljudi z bogvekoliko milijardami povezav), pač pa relacijo prijateljstev oziroma sledenj uporabljata za vse, kar počneta, od priporočanja novih povezav do izbiranja reklamnih sporočil. Pri tem so navadno odkriti in povedo, da nam neko osebo priporočajo v sledenje, ker imamo z njo, na primer, skupne sledilce.

Povezave imajo lahko različne teže: nekatere so močnejše, nekatere šibkejše, saj so si nekateri pari podobni bolj, drugi manj. Povezave z večjo težo lahko upoštevamo bolj kot tiste z manjšo. Če uvedemo uteži, ni več potrebno, da je vsak povezan z določenim številom drugih: povežemo lahko vsakega z vsakim, vendar povezave utežimo s podobnostmi, ki so lahko tudi 0.

Grafov je lahko tudi več hkrati. Twitter prav gotovo ne beleži le, kdo sledi komu in komu so všeč čigavi tviti. Gotovo ga zanima tudi, o čem pišemo: dva uporabnika sta si podobna, če pišeta o podobnih temah. Tako dobimo več relacij podobnosti, ki jih združujemo z različno težo. Poleg tega bodo seveda vključili vse dodatne podatke, ki jih lahko naberejo o uporabnikih — tu nam pride na misel predvsem Google, ki ve o nas vse, od tega, s kom si dopisujemo do (predvsem!) tega, kaj iščemo in katere lokacije obiskujemo.

Izračun podobnosti

V razredu smo podobnost računali preprosto na podlagi skupnega števila izbranih risank. Matematiki bi nas podučili, da se temu reče velikost preseka dveh množic risank.

V praksi bi bila to slaba mera podobnosti, saj bosta imela dva, ki sta izbrala (kupila, poslušala, gledala) veliko stvari, navadno tudi več skupnih stvari, torej bo njuna podobnost precenjena. Običajen način, da upoštevamo število izbranih stvari, je, da število stvari, ki sta jih izbrala oba, delimo s številom stvari, ki jih je izbral vsaj eden. Ali, bi rekli matematiki, velikost preseka delimo z velikostjo unije. Tako definirana podobnost je dovolj uporabna, da si je zaslužila tudi ime: rečemo ji Jaccardova mera.

Za učno uro bi bila takšna definicija podobnosti nerodna, saj bi zahtevala, da ne beležimo le števila skupnih izborov temveč tudi skupno velikost izbora. No, dovolj bi bilo, da bi za vsakega člana skupine vedeli, koliko reči je izbral. Poračunajmo.

Če je nekdo izbral $n_1$ stvari in drugi $n_2$, velikost njunega preseka pa je $m$, je velikost njune unije $n_1 + n_2 - m$: oba skupaj sta izbrala $n_1 + n_2$ stvari, pri čemer pa smo $m$ stvari šteli dvakrat. Njuna Jaccardova podobnost je potem $m / (n_1 + n_2 - m)$. Dovolj je torej poznati velikost preseka in velikost izbora vsakega člana skupine.

V gornji različici smo delo poenostavili tako, da opazujemo le preseke, pri čemer pa smo zahtevali, da vsi izberejo enako število reči, torej $n_1 = n_2 = n$. Jaccardova mera je potem $m / (2n - m)$. Hitro se lahko prepričamo, da bomo s primerjavo velikosti presekov, dobili enak vrstni red po podobnosti kot s primerjavo Jaccardovih mer. Recimo, da je velikost preseka Aninega in Bertinega izbora $m_1$, velikost preseka Aninega in Cilkinega pa $m_2$. Če je $m_1 / (2n - m_1) > m_2 / (2n - m_2)$ je tudi $m_1 > m_2$. O tem se je preprosto prepričati.

$\dfrac{m_1}{2n-m_1} > \dfrac{m_2}{2n-m_2}$

pomnožimo z imenovalcema

$m_1(2n-m_2) > m_2(2n-m_1),$

razpišemo

$2n m_1 - m_1 m_2 > 2n m_2 - m_1 m_2$

odstranimo $m_1 m_2$, ki se pojavlja na obeh straneh, okrajšamo $$2 n$ in dobimo

$m_1 > m_2.$

Če vsi izberejo enako število reči, je vseeno, ali računamo Jaccardovo mero ali presek, saj bo vrstni red po podobnosti enak.

Profili reči in uporabnikov

Sicer pa graf v resnici ni prva reč, ki pride na misel načrtovalcu priporočilnega sistema. Uporabni so za družabna omrežja (mreža oz. omrežje je pravzaprav eden od sopomenk besede graf), manj pa za priporočila v trgovinah in na straneh z glasbo ali videi. Tam uporabnike in reči profilirajo.

V letu 2006 je Netflix objavil anonimizirane podatke za skoraj pol milijona uporabnikov, ki so dajali ocene 18 tisoč filmom. Skupaj se je nabralo 100 milijonov ocen. Slabe tri milijone ocen so skrili in ekipi, ki bi skrite ocene napovedala za več kot 10 % natančnejše od Netflixovega sistema, obljubili milijon dolarjev. Izplačali so ga proti koncu 2009.

Pristop zmagovalcev je temeljil na ideji, da je vsak film mogoče opisati s kakimi 40 lastnostmi. Lahko si predstavljamo, da gre za različne »dimenzije« filma — je smešen, je romantičen, grozljiv, ima lepe posnetke narave, znane igralce, nenavaden scenarij... Koliko film poseduje določeno lastnost, opišemo s pozitivnimi ali negativnimi števili; število, ki opisuje smešnost, bo tem bolj pozitivno in veliko, čim bolj je film smešen, in tem bolj negativno, čim bolj je žalosten.

Hkrati je — tako gre predpostavka — mogoče z istimi 40 lastnostmi opisati okuse. Predvidena ocena filma je potem enaka ujemanju med lastnostmi filma in okusom gledalca. Ujemanju? Kako izračunamo ujemanje? Oceno, ki naj bi jo nek uporabnik dal nekemu filmu, izračunamo tako, da uporabnikovo naklonjenost romantičnim filmom pomnožimo s tem, koliko je film romantičen, k temu prištejemo produkt uporabnikove naklonjenosti grozljivkam in grozljivosti filma, in tako naprej za vseh 40 lastnosti.

Če si v profilih uporabnikov in filmov predstavljamo vektorje, bodo matematiki v tem prepoznali čisto običajen skalarni produkt.

Vendar — kdo bo določil 40 lastnosti in jih ročno vnesel za vsakega od 18.000 filmov? Sploh pa, kdo bo storil isto za pol milijona gledalcev? In kako? Jih bo mogoče intervjuval, da izve, ali so jim bližje komedija ali grozljivke?! Nikakor, prav zato imamo podatke.

Kako je to videti matematično in programersko, opisujemo v dodatku.

En možen pristop je, da vsak film in okus vsakega gledalca opišemo s 40 naključnimi (pozitivnimi in negativnimi) števili v primernem obsegu. S tem, kakšne lastnosti bo predstavljalo teh 40 števil, pa se preprosto ne obremenjujemo. Nato za vsako oceno filma, ki ju dobimo kot ujemanje lastnosti in okusa, preverimo, kako odstopa od prave vrednosti in popravimo (izmišljene!) lastnosti filma ter okus gledalca v smer, ki bo zmanjšal napako. Recimo, da je bila ocena filma previsoka. Pogledamo, v katerih lastnostih je film pozitiven; če naj bi bil smešen, zmanjšamo komponento okusa, ki ustreza smešnosti, saj temu gledalcu smešni film niso všeč. Pogledamo, po katerih lastnostih je negativen: če naj ne bil imel znanih igralcev, potem v opisu okusa povečamo gledalčevo naklonjenost k znanim igralcem, saj bo bo zmanjšalo oceno tega filma. Če je bila ocena filma prenizka, ravnamo nasprotno.

Natančno enako ravnamo s filmom: če je bila ocena previsoka ali prenizka, preverimo, kaj je všeč in kaj ni všeč temu gledalcu in ustrezno spremenimo (domnevne) lastnosti tega filma.

Pravzprav … zgoraj smo govorili o smešnosti in znanih igralcih, čeprav so vsi podatki naključno izmišljeni in smo maloprej pravzaprav sklenili celo, da ne bomo vnaprej določali lastnosti filmov in okusa. Prav v tem je čar. Kaj so lastnosti, nam ni mar. Če bomo šli večkrat (recimo štiridesetkrat) čez vse ocene vseh filmov, bodo te vedno natančnejše. Za tistih štirideset ali koliko lastnosti najbrž ne bomo nikoli vedeli, kaj pomeni posamična od njih, vedeli pa bomo, da odražajo lastnosti filmov in okusov na nek način, smiseln za ocenjevanje filmov.

Vsak film in vsak gledalec je tako opisan s 40 števillkami, ki predstavljajo njegov profil. Kaj pomenijo, ne vemo, vemo pa, da je gledalčevo zadovoljstvo s filmom odvisno od tega, kako se ujemata profil gledalca in filma.

Profili so uporabni še za marsikaj. Par filmov — ali par gledalcev — si je podoben toliko, kolikor sta si podobna njuna profila. Profile lahko uporabimo za to, da poiščemo skupine podobnih filmov; te skupine bodo odražale »žanre«, definirane prek okusov gledalcev. Ali pa poiščemo skupine gledalcev; to utegne priti prav marketinškemu oddelku, ki ga morda zanima, kako čimbolj zadovoljiti potrebe različnih vrst gledalcev.

Podobna ideja profiliranja se — z nekoliko drugačno matematiko — uporabljajo tudi v globokih nevronskih mrežah, s katerimi prepoznavamo, urejamo, iščemo slike, analiziramo besedila … Vendar to res ne sodi več v gradivo o priporočilnih sistemih.

Dodatek: Malo matematike in programiranja

Matematika profiliranja je čisto srednješolska: zahtevala bo odvajanje polinomov druge stopnje. No, pa verižno pravilo. Programiranje pa zahteva gnezdeno zanko; niti pogojnega stavka ne bomo potrebovali. :)

Spodnje besedilo je morda videti strašljivo, a le zaradi notacije.

Naj bo $u$ profil nekega uporabnika, torej 40-dimenzionalni vektor $\overrightarrow{u} = [u_1, u_2, \ldots u_{40}]^T$ in $m$ profil nekega filma, $\overrightarrow{m} = [m_1, m_2, \ldots m_{40}]^T$. Uporabnik je dal filmu oceno $o$, napoved modela pa se izračuna kot skalarni produkt $f = \sum_{i=1}^{40} u_i m_i$. Model je potemtakem naredil napako $e = o - f$.

Opazujmo le en element profila, $u_i$. Kako ga spremeniti, da se bo napaka zmanjšala? Matematično gledano bi rekli, da je ocena $f$ funkcija parametra $u_i$ (in seveda še vseh drugih komponent $u$-ja, vendar se bomo zdajle ukvarjali z eno samo). In seveda je tudi napaka funkcija $u_i$ — če spremenimo $u_i$, se bo spremenila tudi napaka. Pisati smemo torej $e(u_i) = o - f(u_i)$. Zmanjšati želimo absolutno vrednost napake. No, ker je absolutne vrednosti zoprno odvajati, bmo namesto tega raje minimizirali kvadrat napake, $e(u_i)^2 = (o - f(u_i))^2$.

Minimuma ne bomo mogli najti analitično, češ, enačimo odvod s 0 in rešimo enačbo. Uporabili bomo iterativno metodo. Začnemo z nekim približkom. Pogledamo odvod funkcije v tej točki. Če je pozitiven (funkcija narašča) gremo za en droben korak levo, če negativen (funkcija pada), pa za en droben korak desno.

Potrebujemo torej odvod tega, kar bi radi zmanjšali, odvod (kvadrata) napake. In to po $u_i$, saj bi radi zmanjšali napako tako, da izboljšamo $u_i$.

$\dfrac{de^2}{du_i} = \dfrac{d(o - f)^2}{d u_i} = -2(o - f) \dfrac{df}{du_i} = -2e \dfrac{df}{du_i}$

Najprej smo razpisali $e^2$ v $(o - f)^2$, nato odvedli, kot se pač odvede kvadrat: iz $(o - f)^2$ smo dobili $2(o - f)$. Vendar ne smemo pozabiti, da je tudi $f$ funkcija $u_i$, torej moramo uporabiti verižno pravilo: pomnožiti moramo še z odvodom $f$ po $u_i$. (Minus na začetku, pred dvojko, pa zato, ker odvajamo $o$ minus $f$.) Za konec smo se spomnili še, da $o - f$ ni nič drugega kot napaka, $e$.

Ostal nam je še odvod $f$ po $u_i$. Spomnimo se, da je $f(u_i) = \sum_{i=1}^{40} u_i m_i$ ali, če ga razpišemo, $u_1m_1 + u_2m_2 + \ldots + u_im_i + \ldots u_{40}m{40}$. Ob odvajanju tega se ne bomo pretegnili: če odvajamo po $u_i$, je edini člen, ki ni konstanten, $u_im_i$. Odvod $u_im_i$ po $u_i$, pa je pač $m_i$.

$\dfrac{df}{du_i} = m_i$

Vstavimo to v zgornjo enačbo in dobimo

$\dfrac{de^2}{du_i} = -2em_i$

Rekli smo, da bomo šli za majhen korakec v smeri nasprotni odvodu. Ker bo smer nasprotna, odstranimo minus, in ker bomo šli za majhen korakec, zamenjajmo $2$ z $\epsilon$; ta bo enak, recimo 0.001.

Da torej popravimo i-to komponento profila, spremenimo $u_i$ za $\epsilon e m_i$ (minus iz $-e m_i$ je izginil, ker gremo v smeri nasprotni odvodu). Enako naredimo za vseh 40 komponent profila uporabnika in za vseh 40 komponent profila filma. Tako smo izboljšali profil enega uporabnika in enega filma — glede na oceno, ki jo je dal ta uporabnik temu filmu. Enako storimo za vse ocene, ki jih je dal katerikoli uporabnik kateremukoli filmu.

Postopek bo seveda plesal sem ter tja — enkrat bo popravil profil enega filma glede na enega uporabnika, drugič glede na drugega. To je pričakovati: nek film se zdi nekomu bolj smešen, drugemu bolj romantičen. Nič ne de. Naredimo torej za vse ocene vseh filmov. Potem gremo čez vse še enkrat. In še enkrat. In še enkrat … dokler se postopek ne ustali v nekem minimumu.

Postopek je res preprosto sprogramirati.

Takole bi bila videti (zelo psevdo) funkcija, ki prejme oceno nekega filma s strani nekega uporabnika in pripadajoča profila, ter popravi profila:

Funkcija popravi_profil(ocena, u, m):
  napoved = 0
  za vsako komponento i profila uporabnika
    napoved += u_i * m_i
  napaka = ocena - napoved

  za vsako komponento i
    u_i += epsilon * napaka * m_i
    m_i += epsilon * napaka * u_i

Funkcijo pokličemo večkrat, pa bodo ocene počasi skonvergirale. Celoten program je torej tak:

za vsakega uporabnika sestavi naključni profil
za vsak film sestavi naključni profil

dokler se skupna napaka znatno manjša
  za vsako znano oceno
    pokliči popravi_profil(ocena, uporabnik, film)

Vrnimo se k matematiki in razmislimo, kaj se dogaja.

Imamo matriko ocen, recimo ji $\textbf{O}$. Vrstice predstavljajo uporabnike, stolpci filme: element $\textbf{O}_{k,l}$ vsebuje oceno, ki jo uporabnik $k$ da filmu $l$. Matrika je torej ogromna (na primer $500.000\times18.000$) in večinoma prazna, saj večina uporabnikov ni pogledala večine filmov.

Zložimo vektorje profilov uporabnikov v matriko (imenujmo jo $\textbf{U}$), enega pod drugega. Ta bo imela toliko vrstic, kot je uporabnikov in 40 stolpcev. $k$-ta vrstica je profil $k$-tega uproabnika. Zložimo profile filmov v stolpce matrike, ki jo bomo imenovali $\textbf{M}$; $l$-ti stolpec je profil $l$-tega filma. Če zmnožimo $k$-to vrstico $\textbf{U}$ z $l$-tim stolpcem $\textbf{M}$, dobimo napoved ocene, ki jo je uporabnik $k$ dal filmu $l$ — točno to, kar smo računali zgoraj s funkcijo $f$.

Če pomnožimo matriko $\textbf{U}$ z matriko $\textbf{M}$, dobimo matriko napovedi ocen, ki jo bomo imenovali $\textbf{F}$. Naš optimizacijski postopek je iskal takšni matriki $\textbf{U}$ in $\textbf{M}$, da je bil njun produkt čim bližje matriki ocen $\textbf{O}$.

Matriko $\textbf{O}$ smo torej razbili, tako da je $\textbf{O} \approx \textbf{U} \textbf{M}$. Temu rečemo matrična faktorizacija. Njena lepota je v tem, da smo

1. Dobili profile filmov in profile uporabnikov. To lahko uporabimmo tudi za analizo uporabnikov, določanje žanrov filmom...
2. Zmanjšali velikost podatkov. Prej smo imeli 500.000 uporabnikov in 18.000 filmov, torej 9 milijard ocen. Zdaj imamo 500.000 uporabnikov in 40 lastnosti, 18.000 filmov in 40 lastnosti, torej malo več kot 24 milijonov števil.
3. Predvsem pa: matrika $\textbf{O}$ je bila precej prazna — in naša naloga je bila napovedati, kakšne ocene bi uporabniki dali filmom, ki jih še niso videli. Matrika $\textbf{F}$ je polna, saj lahko vsak element izračunamo kot produkt dveh vektorjev — ene vrstice iz prve in stolpca iz druge matrike.

Postopek je davno, še preden je bil Netflixov izziv končan, lepo opisal Simon Funk V njegovem opisu najdemo tudi koščke kode (v C-ju).