Data Mining @ BCM

Chapter 1: Orange Workflows

Orange supports the analysis of data through the construction of workflows. Orange workflows contain components that read, process and visualize data and models. We refer to these components as "widgets." We place the widgets on a "canvas" drawing board to design a workflow. Widgets communicate by sending information along their communication channels. We construct workflows by linking the output of one widget to another widget's input.

A simple workflow with two connected widgets. The outputs of a widget appear on the right, while the inputs appear on the left.

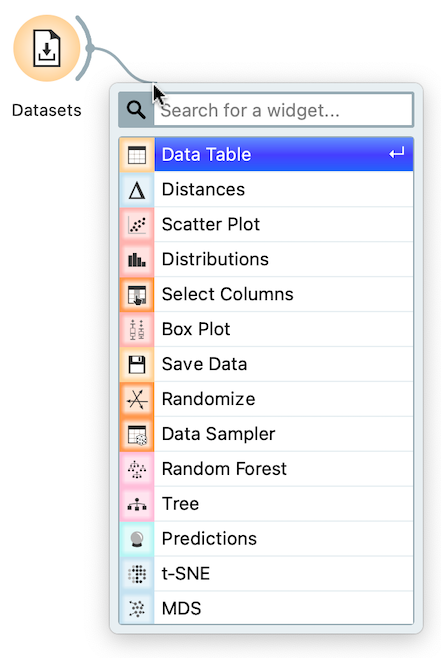
We construct workflows by placing widgets onto the canvas and connecting them by drawing a line from the transmitting widget to the receiving widget. There are several ways to place a new widget on the canvas:

• click on the icon of a widget in the widget toolbar, and the new, unconnected widget will appear on the canvas,
• right-click on the empty space of the canvas, search for the widget by typing a part of its name, and select the widget of choice,
• drag a line from the output or an input of a widget to some empty space on the canvas; just like above, a menu with a list of widgets appears.

The widget's outputs are on the right and the inputs on the left. In the workflow above, the Datasets widget sends its data to the Data Table widget. The Datasets widget loads the data from Orange's datasets server and then pushes the data to the Data Table. Data Table displays the data from its input in a spreadsheet-like form. Don't confuse Data Table with spreadsheet programs like Excel: Data Table only shows the data and is not a data editor. To change the data, one would need to go to its source file, change the data there, and then reload it into Orange. There are, of course, Orange widgets to change and transform the datasets, but we will introduce them later in this guidebook.

If you are using Orange for the first time, the Datasets widget did not load any data yet. Constructing the above workflow with Datasets and Data Table will result in the dashed connection between the two widgets:

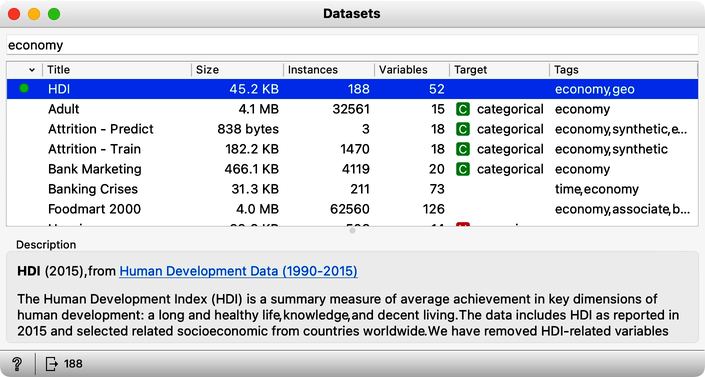
With the dashed connection, Orange tells us that the widgets are connected, but no information is transmitted through the channel. Namely, we have yet to tell the Datasets widget which data to load. Let us double-click the Datasets widget to get its content. The widget displays the list of available data sets. Find HDI, the Human Development Index dataset, and load the data by double-clicking on its row or pressing the return key when the row is selected.

Now, the line between Datasets and Data Table becomes solid, and it is time to check what the loaded data looks like. Let us double-click on the Data Table widget to reveal its contents.

The human development index dataset includes 52 features and two meta variables. The meta variables store the country's name and the HDI index, and the features profile the countries with various socioeconomic indices. Although also just a number, like all other features, we set the HDI index as a meta as it is computed from all other features. We will learn about assigning different roles and types to variables in the following chapters of this guide.

The first few features in the HDI dataset report on life expectancy, mean years of schooling, and gross national income. In which country should we live for the most extended lifespan? Where do people spend the most years in schools? Are these two features related? Do you have to go to school longer to earn more? Well, not everything can be answered in the Data Table, but certainly, we can find the answers to the first two questions. Sort the countries according to the features by clicking on their corresponding header. Do the results surprise you? We can visualize the data in a scatter plot to find the answer to the third question. Let us add the Scatter Plot widget to the workflow and open the Scatter Plot widget by double-clicking on its icon.

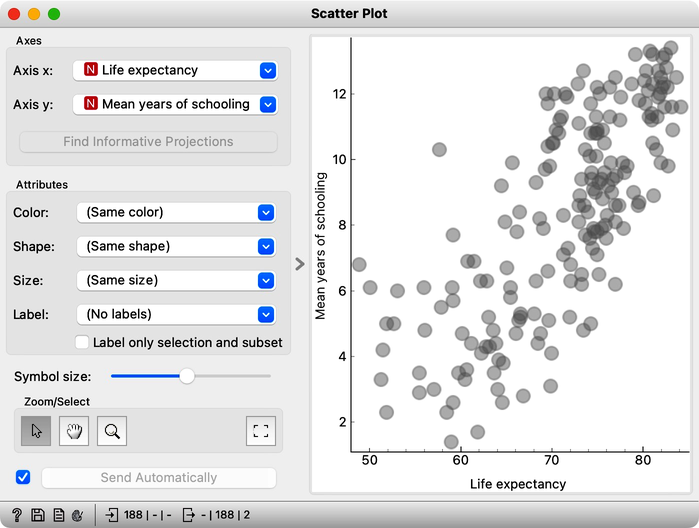
Life expectancy seems to be related to years spent in school. The longer we go to school, the longer we live? Well, not necessarily. Causality and correlation should not be mixed. It would still be interesting to see which countries have the most elaborate school systems and where people live longest. At this stage, we can

• hover over the data point to find which country it represents,
• switch on the data point labeling by selecting country from the Label pull-down menu,
• select a few countries of interest and feed the data to the data table.

Let us go with the third option. We will first connect a new Data Table to the output of the Scatter Plot. Remember, we can do so by dragging a new connection from the Scatter Plot widget and choosing Data Table from the drop-down menu when we release the mouse:

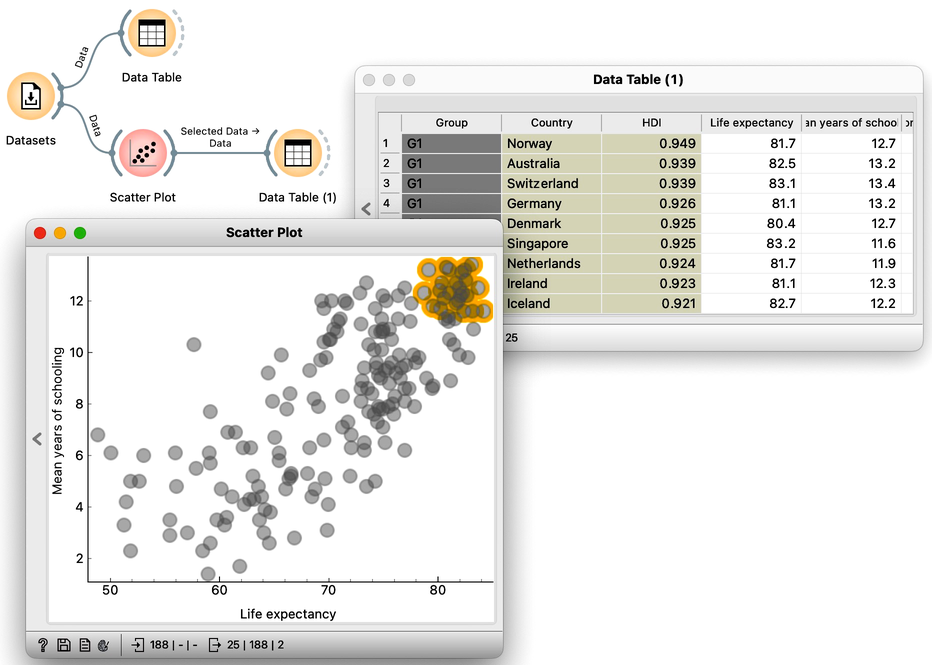
A resulting workflow now contains four widgets. The widget Datasets loads the data, sends it to Data Table, which displays the complete data set, and to Scatter Plot, which visualizes the data for a chosen combination of two features. The Scatter Plot sends selected data to the Data Table (1):

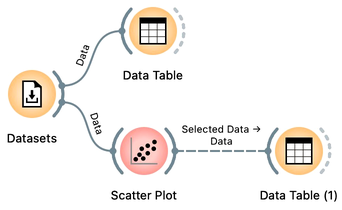
Why is the connection between the Scatter Plot and the downstream Data Table dashed? Oh, we still haven't sent any data between the two widgets! Let's do this while observing Scatter Plot and Data Table (1) side by side.

Two technical remarks.

• In the screenshot above, we have collapsed the left part of the widget by clicking the area that separates it from the main part of the widget. To expand it again, we click the remaining strip on the left edge of the widget's window.
• Every time we click on Orange's canvas, the canvas window comes up front and hides the widgets. We can bring the windows of the opened widgets to the front by choosing Bring Widgets to Front command from the View menu or pressing Ctrl-Down on Windows or Cmd-Down on mac. In the same menu, we can also choose to always to display widgets on the top.

After selecting the points in the Scatter Plot, the dashed connection between the Scatter Plot and Data Table (1) widget icons becomes solid: the Scatter Plot has provided the data on this connection. Single-clicking on the empty part of the scatterplot removes the selection selection and clears the output.

Any change in the selection of the Scatter Plot points propagates through the workflow and updates the display in the Data Table (1). This mechanism is excellent: we have just constructed our first combination of widgets for exploratory analysis. Use it to find the countries with the lowest lifespan. Or the country in the upper left quadrant of the scatter plot display that looks like an outlier. Do countries in different groups belong to some different geographical regions?

We can select a data subset in most of Orange's widgets that visualize data, including the Data Table. Let us remove Scatter Plot and Data Table (1) widgets and add another widget at the existing Data Table's output. We can remove a widget by:

• right-clicking on its icon and selecting Remove from the pull-down menu,
• selecting it by clicking the icon, and then pressing delete or backspace key, or
• dragging a rectangle around a group of icons of widgets we would like to remove and then pressing the delete or backspace key.

Our workflow should now contain three widgets:

Open Data Table and Data Table (1), and select some data items (rows) in the Data Table. Notice how the selection of rows propagates to the Data Table (1):

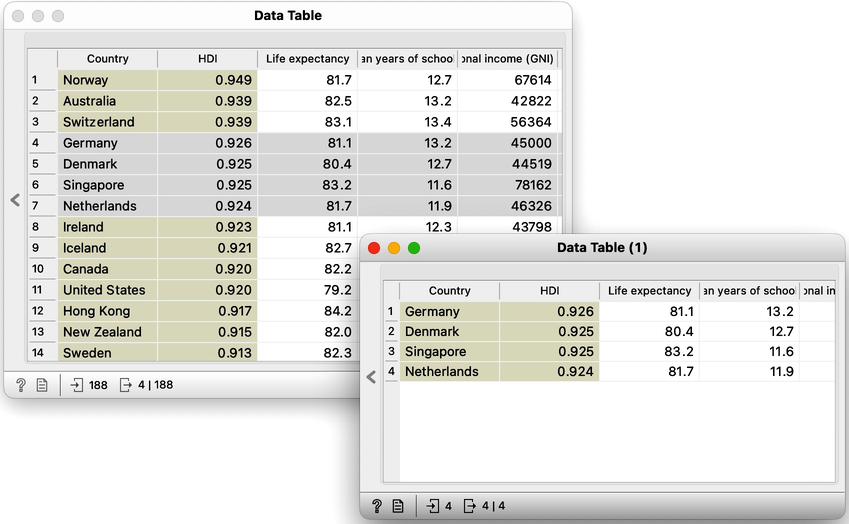
Rather but not entirely useless. If the first Table is sorted by some criteria, the row numbers are shuffled as well. The second table shows the same data, but re-enumerated.

While this, we hope, is instructive from the point of view of Orange mechanics, displaying the selection from one Data Table in another Data Table is rather useless. It would be much more interesting to select rows in the Data Table and highlight the selected data items in the Scatter Plot. This way, we could sort the data by country name, choose our featured states, and find where they are in the Scatter Plot. Let us do so! We can remove Data Table (1) and a Scatter Plot and then (and only then) connect the Scatter Plot to the Data Table:

We can now open both Data Table and Scatter Plot widget and browse through countries in the Data Table, selecting those of interest and checking out how well they do in the Scatter Plot.

The workflow above implements another exploratory data analysis combined with two widgets. And we have just started our Orange data science journey! For our last workflow, we learned that widgets could accept multiple inputs. Scatter Plot can receive data as well as a data subset. Double click on any of the links in the workflow to view what kind of signals widgets can output and what they can receive on the input. The details between the communication link between Data Table and Scatter Plot, for instance, show that the Scatter Plot widget has three input channels, and Data Table two:

What does the Features channel of Scatter Plot do? And who can output this type of signal? Read on.

Chapter 2: Saving your Work

Let us show you how to save your work in Orange. Before we do this, we will build a workflow and demonstrate a few more tricks for Orange’s visual programming. We will use the same socioeconomic data as in the previous chapter, Workflows. This time, however, we should add the instance of the Datasets widget without using the toolbox. To add the instance of the Datasets widget, we can right-click on canvas, type, say, "data," which will show me the Datasets widget, and, with its row highlighted, press return.

Opening the widget, we see that the HDI data set is already loaded – notice the green dot next to its name - assumming, of course, that you have followed the lectures from the previous chapters in these notes. Orange widgets remember our previous choices and actions. For example, we can check the data in the Scatter Plot to see that it still displays the pair of features that we have last observed.

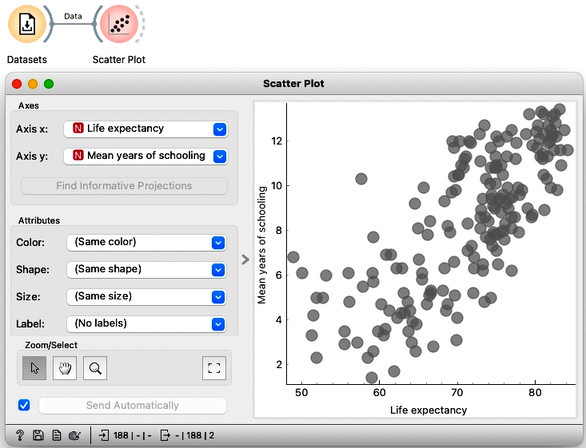
It does. The last time we have used the Scatter Plot was to display the relation between life expectancy and years of schooling. To add some more content on our workflow, let's find, say, my country, Slovenia, on this map. We could add the point labels to the plot, but then this visualisation becomes too crowded. One widget to easily find the specific countries is for instance Data Table, where we will sort the countries by name. The Data Table outputs data instances corresponding to rows I select in this widget. First, we can check if this is so by connecting another instance of the Data Table. Everything is fine; Slovenia is the only country displayed in the Data Table (1). We can can go back and select, say, Spain as well by pressing on the Command modifier key before clicking. Great, we now have Slovenia and Spain on the output.

Fine. We no longer need Data Table (1) in our workflow. We can select it and press Delete or Backspace to remove this widget, or right click the widget and choose remove.

Our intermediate goal here is to highlight the countries chosen in the Data Table and highlight them in the Scatter Plot. We can connect the output of the Data Table to the Scatter Plot. Notice that Orange knows that the Scatter Plot already has Data on its input and plugs the new connection into a "Data Subset" channel of the Scatter Plot. The Scatter Plot now has two highlighted points in the upper right quadrant. We can now show the country labels but display them only for an input data subset.

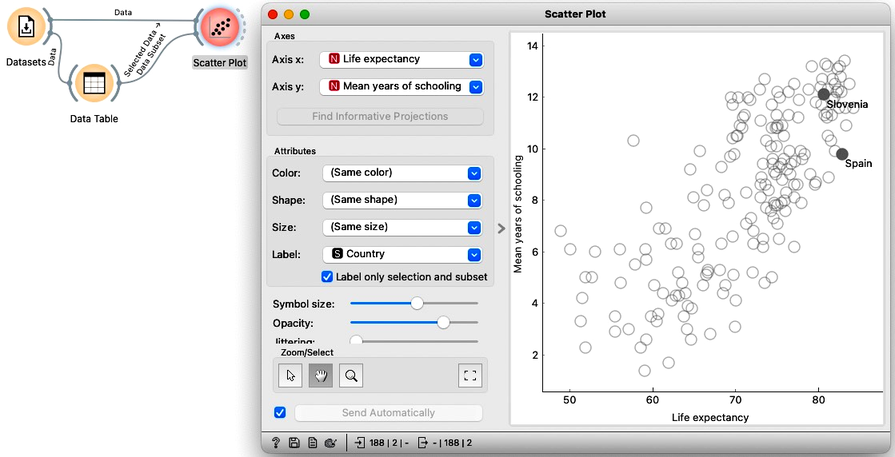
We can now change the selections in the Data Table and observe the countries' positions in the Scatter Plot. For example, Singapore is on the right, Romania is up top, and Sierra Leone is below. The countries with the highest income are all in the top quadrant.

Finally, back to what we have promised in the title of this section. We can now save our work by choosing Save from Orange's File menu. Let us save the workflow in the "countries" file, which we will place on the Desktop. We can now quit Orange and return to our saved work later.

Chapter 3: Correlations

The purpose of this section is to show that not all Orange widget channels carry the data. We will demonstrate this on the Human Development Index and by exploring the correlations between data features.

The most common communication item carried from one widget to another is the data table, denoted with "Data".

Namely, in all our previous workflows, Orange widgets sent data instances to one another. For example, we loaded the Human Development Index data with the Datasets widget and then looked at the data in the Data Table. Notice that Orange reports that the two widgets communicate using the Data channel. We also used the Scatter Plot, and again the output carried from the Datasets widget is labeled as “Data”.

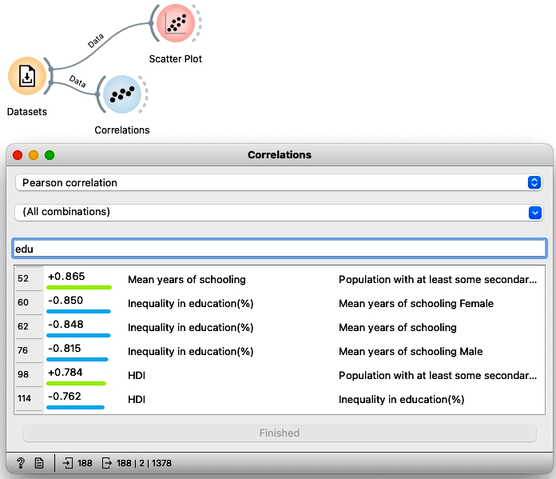
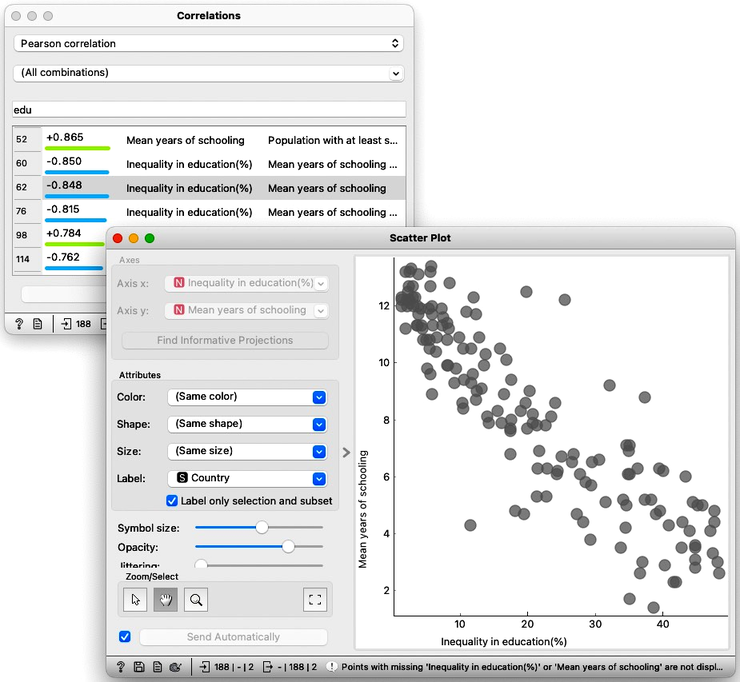
But the information carried from one widget to another does not necessarily contain only the data instances. For example, Orange widgets can also output distance matrices, objects that learn from the data, evaluation results, or a set of data features. We will learn about these and other types of channels later, but let us show an example here. We will use the Correlations widget that displays correlations between pairs of features in the data set. The widget sorts the feature pairs by the absolute correlation. We can see that some features in Human Development Index data are strongly correlated. For instance, countries with high infant mortality rates have also high mortality rates for kids. More interestingly and besides the most obvious correlations, inequality of education is negatively correlated with mean years of schooling.

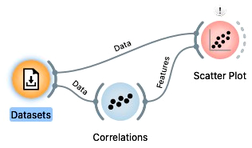
We would like to display each particular relation between two widgets in the Scatter plot. We could open a Scatter plot, and manually find this particular pair of features, but we would need to do this for every pair we find interesting in the Correlations widgets. Instead, we can connect Correlations to the Scatter Plot. Orange asks us what type of connection we prefer. We do not want Correlations to emit the data with only the chosen set of two features, so we click on the link and cancel this signal. Instead, we see that Correlations also outputs the information on the two features that I can select in the widget, and the Scatter Plot can receive this information on the Features channel. Let us establish this communication channel by dragging a line from the Features box of Correlations to the Features box in the Scatter Plot.

Replay

Correlations widget emits a tuple of features to the Scatter Plot.

We can see that Orange now adds the label Features on the link between Correlations and Scatter Plot. We can now open both widgets side-by-side; selecting a row in Correlations now emits a signal that informs the Scatterplot which axis to display. We can, for instance, see why inequality of education is negatively correlated with mean years of schooling, or why there is such a high correlation between male and female populations with at least some secondary education.

Chapter 4: Distributions

Let's get familiar with more visualisations by further exploring the Human Development Index (HDI). We start with distributions and add the Distributions widget to the Datasets.

Load the HDI data in the Datasets widget. See the previous chapter for the details.

A widget similar to Distributions is a Violin Plot. We will skip it in this introduction but encourage you to use it and compare it to the Distributions widget.

Distributions display a histogram of values of selected features. For example, the life expectancy distribution is skewed to higher values, and life expectancy is low only in a few countries. You may want to change the bin width to obtain the visualization below.

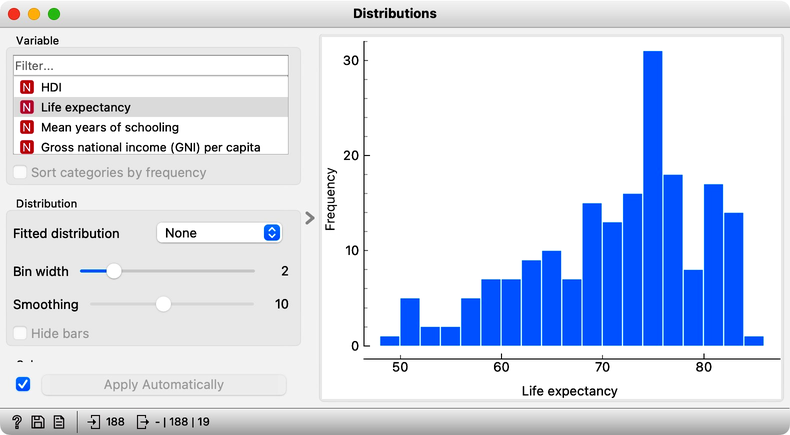
Here, it is worthwhile to go through other features of interest and check their distribution. We continue our example with the distribution of the Human Development Index, which looks almost uniform and select data where this index is high in the distribution widget. We perform this selection by clicking and dragging through the histogram bars. For a start, let us check the output of the Distribution widget in the Data Table:

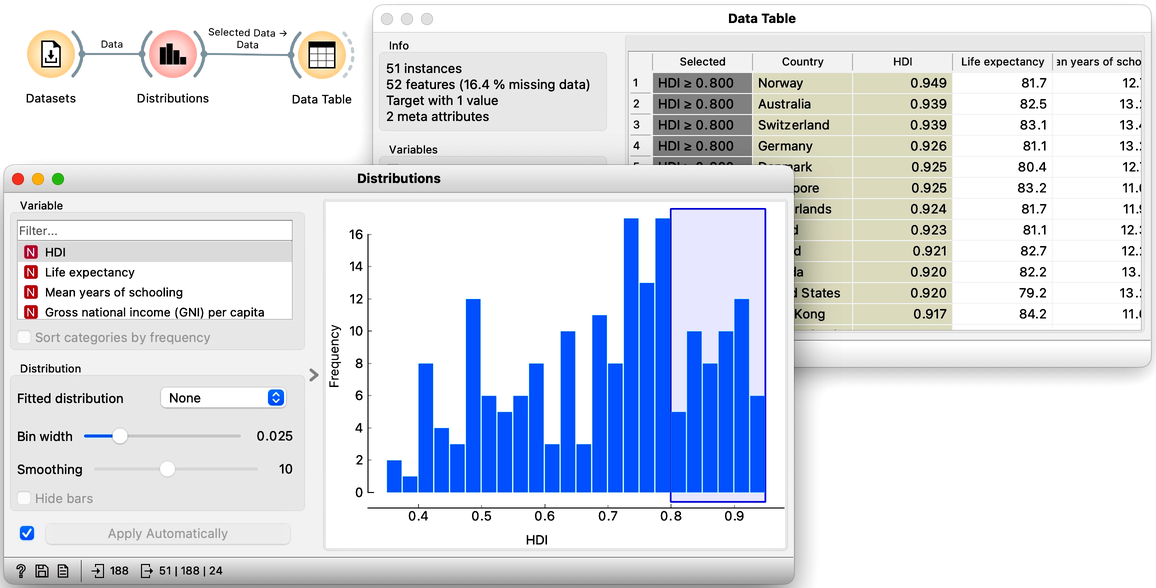
Again, notice that any data selection changes in the Distributions widget propagate through the workflow and trigger an update in the Data Table. Perhaps more interesting is the following combination with a Scatter Plot widget.

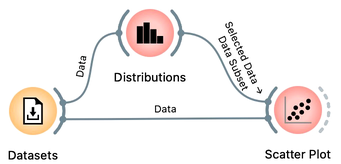
We aim to see where the countries with high or low human development index (whatever we selected in the Distributions widget) are displayed in the Scatter Plot. For instance, most of the countries with high development index have a developed education system and high life expectancy:

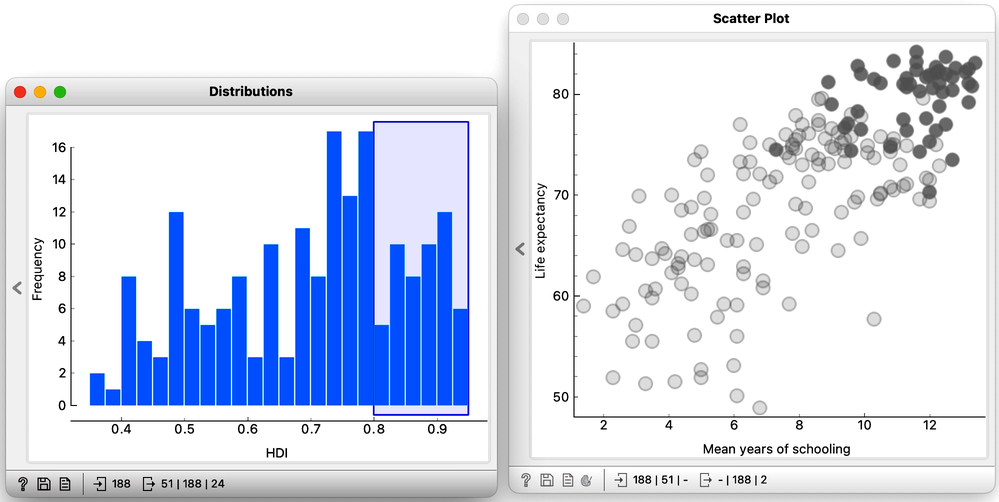
For an even more dynamic demonstration, we can (perhaps with a bit wider bins) select one bar in the histogram and press right and left on the keyboard to see the corresponding countries in the scatter plot.

Replay

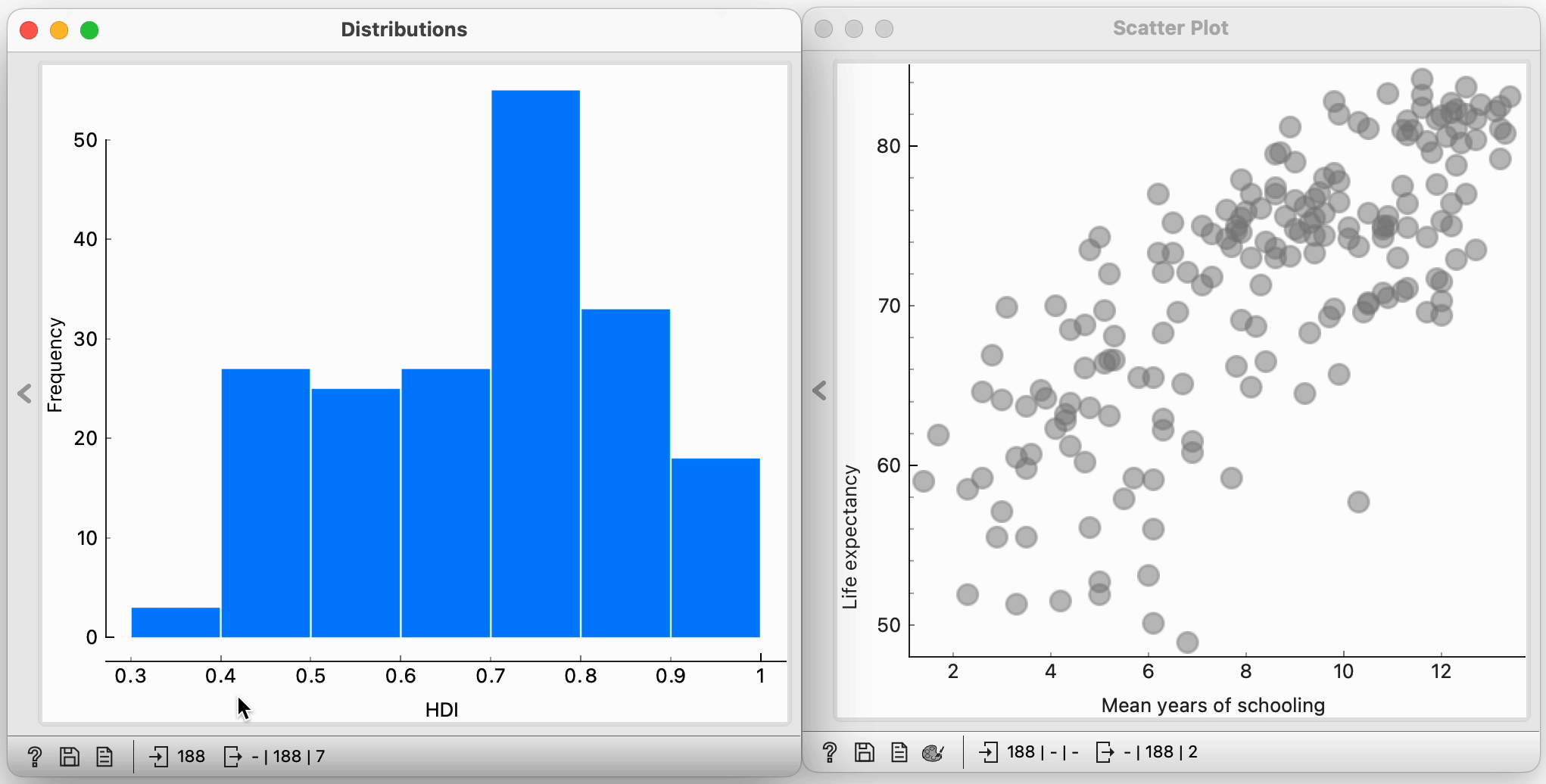
Most countries with a high human development index are in the upper quadrant of the life expectancy-schooling plot, though not entirely. There is, however, some overlap. For instance, some countries with high mean years of schooling have a low human development index. It would be interesting to compare the distributions of years of schooling for countries with low and countries with high development index. We can do this, and here is the trick: we will construct the workflow with two Distributions widgets. In the first one, we will select the countries with a high development index, and push the information about this selection, together with the data, to the second Distributions widget. To start with, here is the workflow:

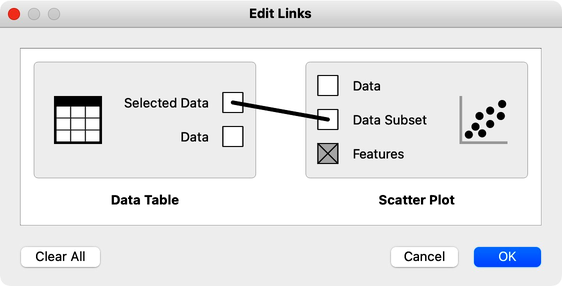
Double-clicking the link between the widgets opens an Edit Links window. Click on the solid line to remove the link, or drag a line from a square representing the output channel of one widget to the square representing the input of the other widget.

Notice that if we drag the link between the Distribution widget and the Data Table widget, Orange will, by default, connect the Selected Data output channel. In the workflow above, we changed this setting by double clicking on the link between the two widgets any rewiring the connection to link the Data output of the Distributions widget with the Data input of the Data Table widget:

Replay

The Data output of the Distributions widget carries out the entire data set but includes a special feature called Selected that reports if the data instance was selected or not.

We have changed the link for the Data Table and for the Distributions (1) widgets. Opening a Data Table widget reveals that the Distribution widget added two features to our data set: the Selected feature and a feature called Bin. We will use the Selected feature here, as it reports if the country was or was not selected in the Distributions widget. The Selected is a two-valued feature, with values Yes and No:

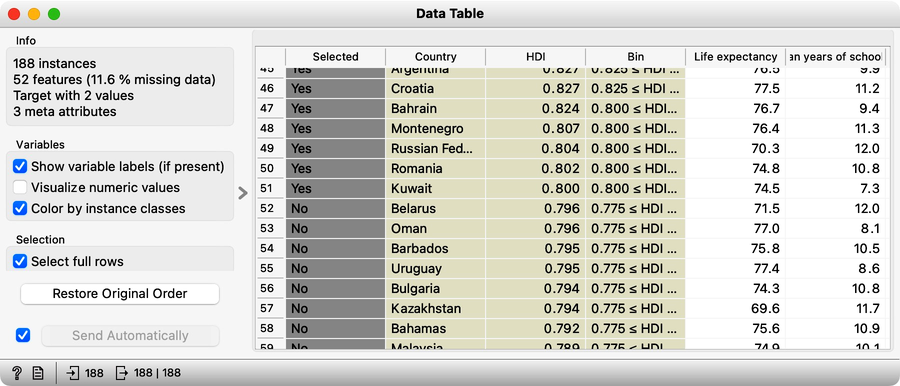
We used Data Table in our workflow to check what the data on the output of the Distributions widget looks like. It is always good to observe any raw, augmented, or transformed data in the Data Table prior to the analysis to verify that everything looks all right and to understand the outputs of the Orange widget. Now that we know about the presence of the indicator feature Selected, we can use it in Distributions (1) to split the data and observe conditional distributions:

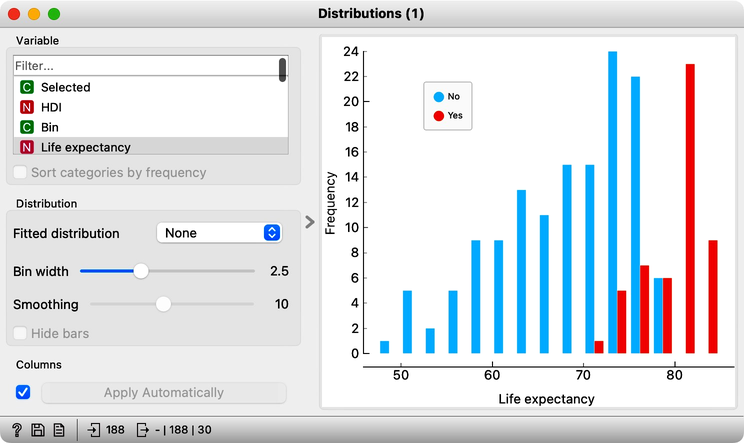
The overlap is now clearly visible, and so is our previous observation that only the countries with high life expectancy have a higher human development index. You can observe conditional distributions of other variables and perhaps observe that the differences in the distributions are indeed pronounced with some of the variables and are less apparent with the others.

A widget similar to Distributions but with a different presentation of the variability of values is a Box Plot. Let us add it to the workflow and use it to confirm our previous findings. Again, we will rewire the link to this widget, remove the connection from Selected Data and connect the Data channel output from the Distributions widget. Make sure to choose Selected for subgrouping the data and observe the differences in life expectancy given our choice of grouping related to the human development index.

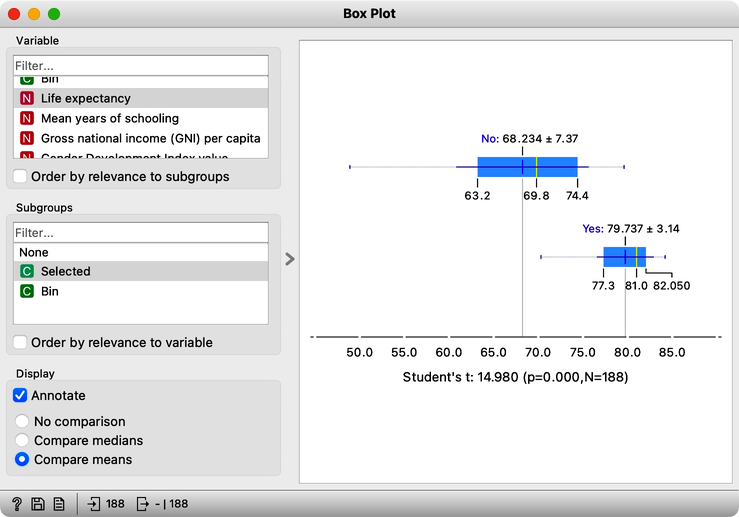
The box plot shows that the mean life expectancy in countries with a high human development index is much higher than in other countries (79.7 vs. 68.2), and there is little overlap between the two distributions. Regarding the overlap: it would be interesting to find features where the differences between the countries with low and high human development indexes are the largest. At this stage, let us consider what we mean by "little overlap". We want the means to be as far away as possible. And we would like distributions with little spread. We could compute the difference of the means and divide it with the root of the sum of the squared variances to get the feature score. This score is, in fact, the Welch's t-test, also displayed at the bottom of the Box Plot visualization. The value of the t statistics for our split of the data and life expectancy is 14.98, a value that would be improbable to obtain if the split between selected and a non-selected group of countries were random (hence p=0.0). Checking the "Order by relevance to subgroups" checkbox orders the features by the p-value. It turns out that features reporting on national income, life expectancy, inequality, and health care quality are most related to the human development index.

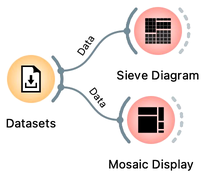
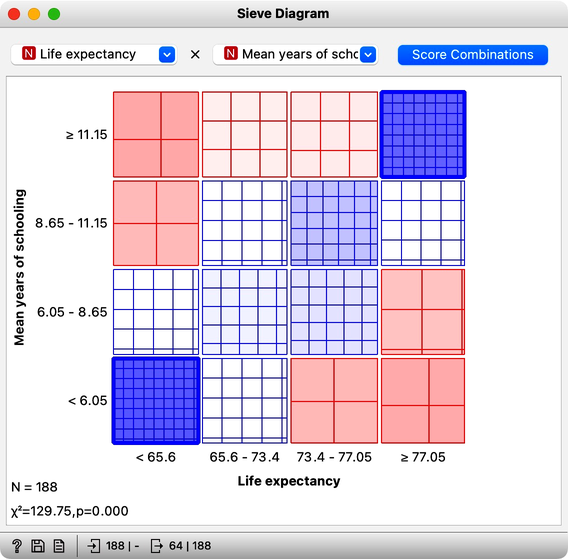
Several widgets in Orange can help us explore joint distributions of two or more variables. One such visualization is a Sieve Diagram, which discrete the continuous variables into four intervals and displays how likely it is to encounter a particular combination of the two features. For schooling and life expectancy, it turns out that the most likely combinations are either with both feature values low or both values high. There are other exciting combinations in this data set, and we encourage you to find them with the Score Combination feature. You may also compare Sieve Diagram to the Mosaic Plot, a somehow more sophisticated widget where you can examine joint distributions of more than two features.

Chapter 5: Data Construction

All of our previous data sets came from Orange’s data set server and to get them, we have been using the Datasets widget. We loaded the data – say, on countries and their socioeconomic indices – and started off by checking it out in Data Table.

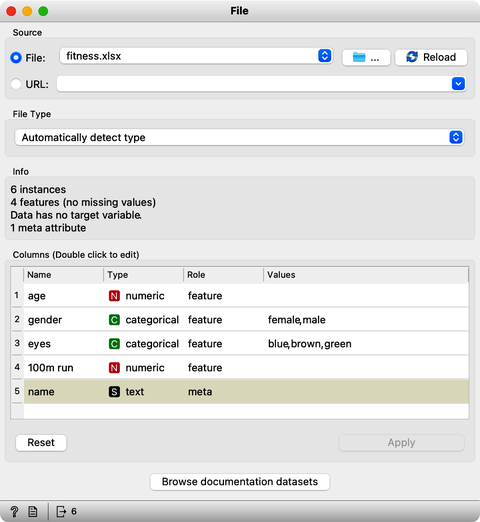
But what if I wanted to use some of my own data? As it turns out, Orange can read tabular data from various sources, including Excel files. So let’s start out by constructing one such data set. Our spreadsheet will include some data on students, and will include the column of names: Jill, Ana, John, Stacey, Mike, and Fred. It will also include a column with student's age, gender, and eye color. Finally, we can add their times for a 100 m run. Here is our spreadsheet we have just created, populated with the values of features for each student.

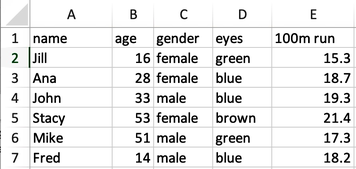
Alternatively from adding a File widget, try dragging the spreadsheet document to Orange's canvas.

Not that this data makes much sense; it is just an example of how to prepare a tabulated data set for any machine learning. We will store the data set I have just created to the desktop in a file, say, fitness.xlsx. Now, we can open Orange, and place a File widget on Orange canvas. Like with other widgets, we used a right click to find this particular widget. Orange comes with some preloaded data sets that I can access from this widget, but right now we are interested in our fitness data. So we can click on the three dots button and find our Excel file. The File widget reports on the data columns, and shows the names of the features.

Orange does actually provide a way to analyze text in the text-mining add-on, but I will skip that for now.

Notice that Orange also detects the feature types. For instance, age is a numerical feature; it stores numbers. The color of the eyes is categorical. Categorical and numerical features profile the students, and we can use them, for instance, to compute distances. We cannot do anything computationally with names stored in the textual meta-feature. Meta features provide additional information about the data instances, for example, to identify them in the scatter plots, but Orange does not use them in any modeling.

Now back to our dataset. The first thing to do after loading the data is to check it out in a spreadsheet. Let us open it in Data Table. Here we find our data just like we set it up in Excel. Let us say we do not need information on eye color. I can use the Select Columns widget and move the eyes from the list of features to the Ignored box. Checking the data in a new Data Table I indeed find no eye colors here.

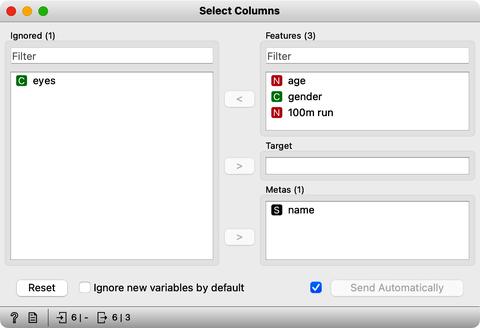
The Select Columns widget is a great widget to manually edit the data domain and play with including and excluding features. We will use it from time to time in our next videos. Moving on we would now like to save my edited data set.

This can be easily done with the Save Data widget: we just click Save As, choose to save our data in, say, an Excel file, and rename the file to fitness-no-eyes, as creepy as it sounds. This file can also just go on our desktop for now.Taking a look at the file I can double-click it to view it in Excel.

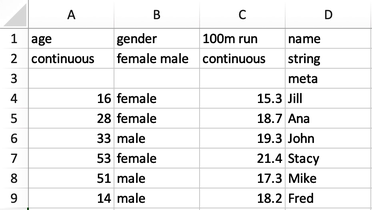
Notice that apart from the feature names, Orange also stored some data on the feature types in the second and third rows. Saving of this extra info can be toggled on or off in the Save Data widget.

Now we know how to prepare some of our own data for Orange. And we also know how to export data from Orange. Note, again, that every time we prepare our own data sets, it is just good practice to first check it out in Data Table. In our running example, we used Excel, but Orange also loads tab- or comma-separated data sets as well as data sets in a bunch of other formats.

Chapter 6: Distances in 2D

Clustering, that is, the detection of groups of objects, is one of the basic procedures we use to analyze data. We can, for instance, discover groups of people according to their user profiles through service usage, shopping baskets, behavior patterns, social network contacts, usage of medicines, or hospital visits. Or cluster products based on their weekly purchases. Or genes based on their expression. Or doctors based on their prescription.

Most popular clustering algorithms rely on relatively simple algorithms that are easy to grasp. In this section of our course, we will introduce a procedure called hierarchical clustering. Let us start, though, with the data and with the measurement of data distances.

We will use the data on student grades. The data is available through Orange’s Datasets widget. We can find it by typing "grades" in the filter box. We can examine this data in the Data Table. Sixteen students were graded in seven different subjects, including English, French, and History.

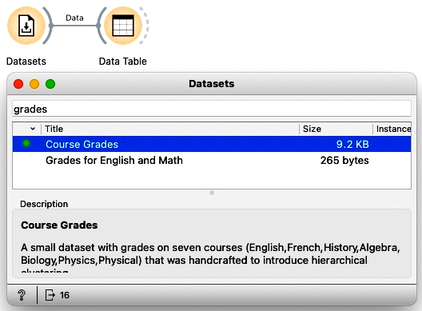
We would like to find students whose grades are similar. Teachers, for instance, may be interested to know if they have students talented in different areas so that she can adjust their training load appropriately. While, for this task, we would need to consider all the grades, we will simplify this introduction to consider only grades from English and Algebra, constructing, in this way, a two-dimensional data set.

To select only specific variables from the data, we can use the Select Columns widget. We will ignore all features except English and Algebra. We can do this by selecting all the features, moving them to the Ignored column, and then dragging English and Algebra back to the Features column. It is always good to check the results in the Data Table.

Here, we selected English and Algebra for no particular reason. You can repeat and try everything from this lesson with some other selection of feature pairs.

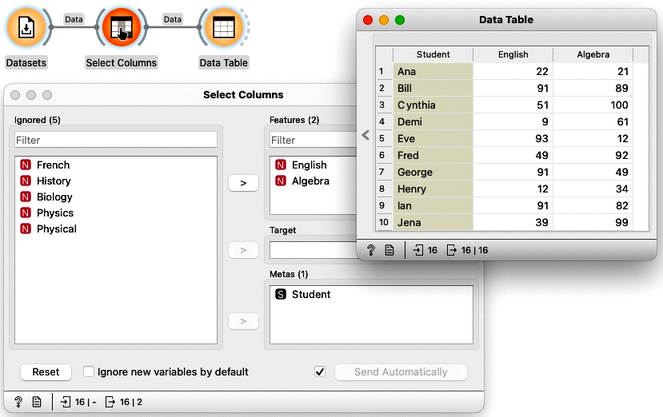
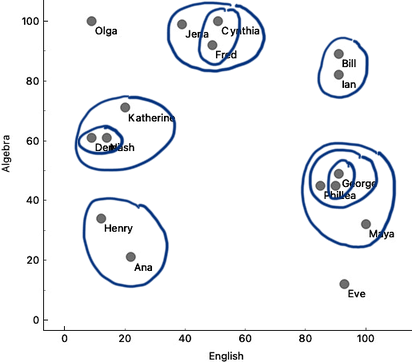
Since we have the data with only two features, it is best to see it in the Scatterplot. We can label the dots representing students with their names.

If all the data on this planet would be two-dimensional, we could do all the data analysis in the scatter plots.

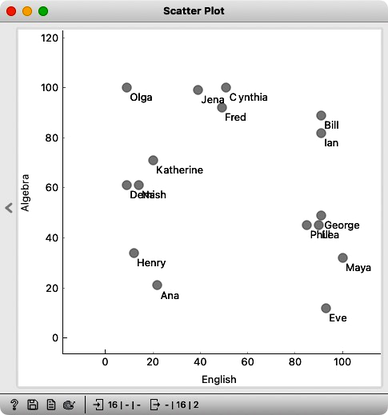
We can see Olga with a high math grade on the top left and Maya in the opposite corner of the plot. They are really far apart and definitely would not be in the same cluster. On the other hand, George, Phil, and Lea have similar grades in both subjects, and so do Jena, Cynthia, and Fred. The distances between these three students are small, and they appear close to each other on the scatterplot.

There should be a way to formally measure the distances. In real life, we would just use a ruler and, for instance, measure the distance between Katherine and Jena by measuring the length of the line that connects them. But since Orange is a computer program, we need to tell it how to compute the distances. Well, Katherine’s grade in English is 20, and Jena’s is 39. Their English grade difference is 19. Katherine scored 71 in Algebra and Jena’s 99. The algebra grade difference is 28. According to Pythagoras, the distance between Katherine and Jena should be a square root of 19 squared plus 28 squared, which amounts to about 33.8.

We could compute distances between every pair of students this way. But we needn't do it by hand, Orange can do this for us.

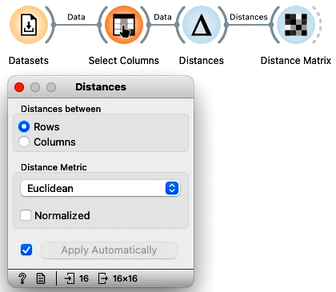
We will use the Distances widget and, for now, remove normalization. The grades in English and Math are expressed in the same units, so there is no need for normalization now. We’ll keep the distance matrix set to Euclidean distance, as this is exactly the one as we have defined for Katherine and Jena.

Warning: the Normalization option in the Distances widget should always be on. We have switched it off just for this particular data set to compare the computed distances to those we have calculated by hand. Usually, the features are expressed in different scales. To jointly use these features in the computation of the Euclidean distances, we have to normalize them.

We can look at the distances in the Distance Matrix, label the columns and rows with student names, and find that the distance between Katherine and Jena is indeed 33.8, as we have computed before.

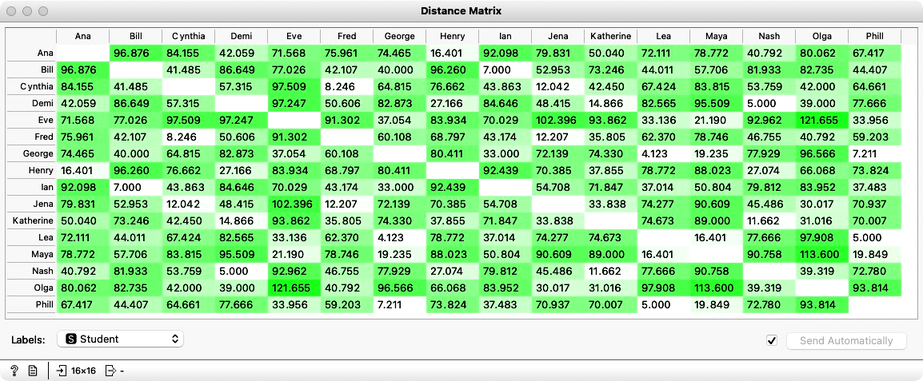
We now know how to compute the distances in two-dimensional space. The idea of clustering is to discover groups of data points, that is, students, whose mutual distance is low. For example, in our data, Jena, Cythia and Fred look like a good candidate group. And so do Phil, Lea and George. And perhaps Henry and Ana. Well, we would like to find the clustering for our entire set of students. But how many clusters are there? And what clustering algorithm to use?

Chapter 7: Cluster Distances

For clustering, we have just discovered that we first need to define the distance between data instances. Now that we did, let us introduce a simple clustering algorithm and think about what else we need for it.

When introducing distances, we worked with the grades data set and reduced it to two dimensions. We got it from the Datasets widget and then use Select Columns to construct a data set that contains only the grades for English and Algebra.

The Hierarchical Clustering algorithm starts by considering every data instance - that is, each of our students - as a separate cluster. Then, in each step, it merges the two closest clusters. Demi and Nash are closest in our data, so let’s join them into the same cluster. Lea and George are also close, so we merge them. Phil is close to the Lea-George cluster, and we now have the Phil-Lea-George cluster. We continue with Bill and Ian, then Cynthia and Fred, and add Jena to the Cynthia-Fred cluster, Katherine to Demi-Nash, and Maya to Phil-Lea-George, Henry joins Ana, and Eve joins Phil-Lea-George-Maya. And now, just with a quick glance – and we could be wrong – we will merge the Bill-Ian cluster to Jena-Fred-Cynthia.

For the two-dimensional data, we could do hierarchical clustering by hand, in each iteration circling the two clusters we join into a group.

Single linkage.

Though, hold on! How do we know which clusters are close to each other? Did we actually measure the distances between clusters? Whatever we have done so far was just informed guessing. We should be more precise.

Say, how do we know that Bill-Ian should go with Jena-Cynthia-Fred, and to George-Phil-Lea and the rest? We need to define the computation of distances between clusters. Remember, in each iteration, we said that hierarchical clustering should join the closest two clusters. How do we measure the distance between Jena-Cynthia-Fred and Bill-Ian clusters? Note that what we have are the distances between data items, that is, between individual students.

Complete linkage.

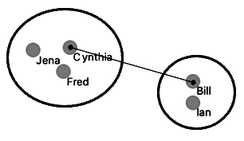
How do we actually make sure what are the distances betwen clusters? There are several ways to measure the distances between clusters. In the simplest, we can define cluster distance as the distance between two of their closest data items. We call this distance a “single linkage”. Cynthia and Bill are the closest. If we use a single linkage, this distance defines the distance between two clusters.

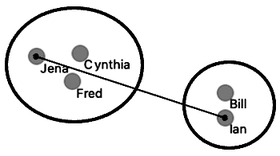
We could also take two data instances that are the farthest away from each other and use their distance to define the cluster distance. This is called “complete linkage”; if we use it, Jena and Ian represent the cluster distance.

In a third variant, we would consider all the pairwise distances, say, between Ian and Cynthia, Ian and Fred, Bill and Cythia, Bill and Jena, Bill and Fred, and from them compute the average distance. This is, not surprisingly, called the “average linkage”.

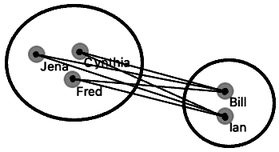Average linkage.

Now we have just defined the second ingredient we need for hierarchical clustering, besides ways to measure the distance between data items, is the way to compute the distance between clusters. Before, when we started to join clusters manually, we used just a sense of closeness, probably something similar to average linkage. Let us continue in this way for just a while.

We will join the Henry-Ana cluster to Demi-Nash-Katherine, and perhaps merge Olga with a cluster on the right. We will then add the top cluster to the one on the bottom right – although here, we do not know exactly which solution is the best. We would need something like Orange to compute cluster distances for me. Finally, we can merge the remaining two clusters.

Here our merging stops. There’s nothing else we can merge. The hierarchical clustering algorithm stops when everything is merged into one cluster. Below is the result of hierarchical clustering on my two-dimensional data set of student grades.

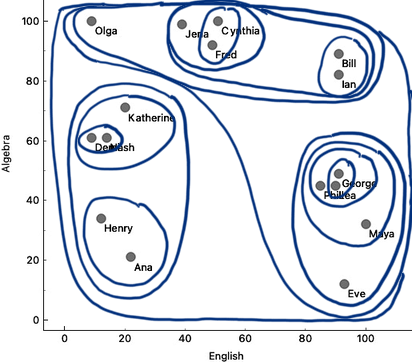
Our depiction of clustering looks, at best, a bit messy, but somehow still shows a clustering structure. There should be a better, more neat way to present the clustering results. And we still need to find a way to decide the number of clusters.

Chapter 8: Dendrograms

So far, we have reduced the data we used in an example for hierarchical clustering to only two dimensions by choosing English and Algebra as oot features. We said we could use Euclidean distance to measure the closeness of two data items. Then, we noted that hierarchical clustering starts with considering each data item in its own cluster and iteratively merges the closest clusters. For that, we needed to define how to measure distances between clusters. Somehow, intuitively, we used average linkage, where the distance between two clusters is the average distance between all of their elements.

In the previous chapter, we simulated the clustering on the scatter plot, and the resulting visualization on the scatter plot was far from neat. We need a better presentation of the hierarchical clustering results. Let's, again, start with the data set, select the variables, and plot the data in the scatter plot.

Let's revisit the English-Algebra scatter plot. When we join the two clusters, we can remember the cluster distance and plot it in a graph. Say, we join George and Lea, where their distance is about 5. Then we could add Phil to the George-Lea cluster, with the distance, say, 6. Then Bill and Ian with a distance of 7. And then, a while later on, I add Maya to Phil-Lea-George at a distance of 15. We can represent this merging of the clusters in a graph, hand-drawn here in the depiction below.

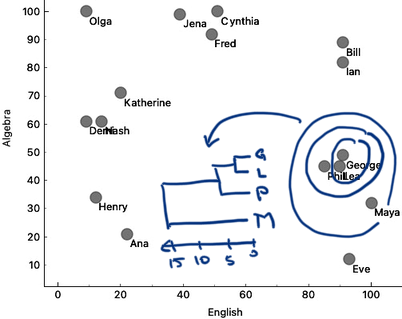
The cluster merging graph that we are showing here is called a dendrogram. Dendrogram visualizes a structure of hierarchical clustering. Dendrogram lines never cross, as the clustering starts with clusters close to each other, and cluster distances we find when iteratively merging the clusters grow larger and larger.

To construct hierarchical clustering in Orange, we first need to measure distances. We have done this already in a previous chapter, where we used Distances widget. We will use Euclidean distance, and only for this data set, we will not normalize the data. We now use these distances, send them to Hierarchical Clustering widget and construct the dendrogram.

We are still working on the two-dimensional data set, hence the use of Select Columns to pick only English and Algebra grades from our example dataset.

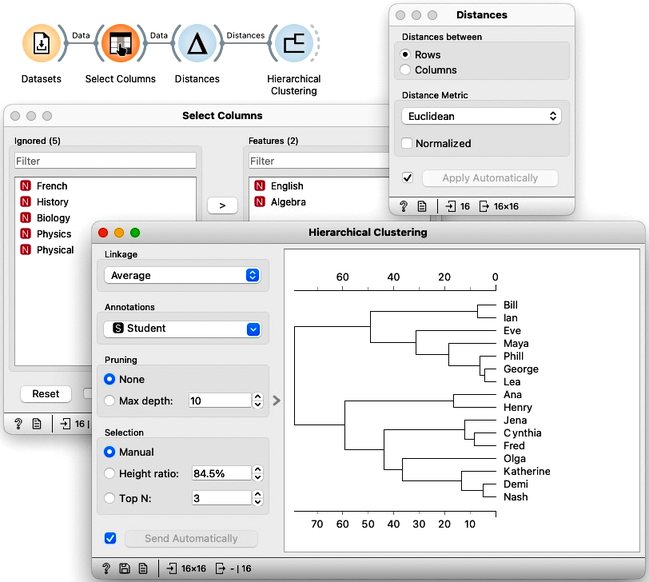
We may remember from our writing on distances that Lea, George, and Phil should be close, and that Maya and Eve join this cluster later. Also, the distance between Bill and Ian is small, but they are far from the George-Lea-and-the-others cluster. We can notice all these relations, and inspect the entire clustering structure from the dendrogram above.

We can now cut the dendrogram to expose the groups. Here, we cut it such that we get three clusters. Where are they in the scatter plot? The Hierarchical Clustering widget emits the Selected Data signal. Here, by cutting the dendrogram, we selected all the data instances, so it should also include the information on the clusters.

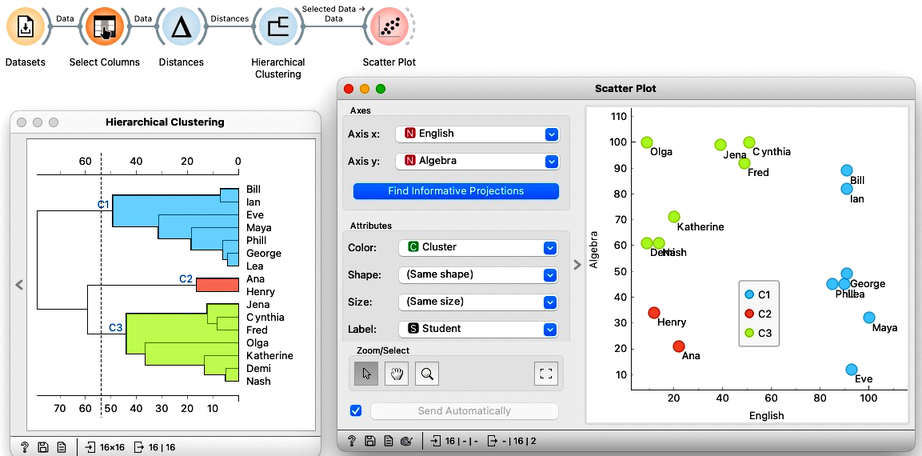
We can use this workflow to experiment with the number of clusters by placing the cutoff line at different positions. Here is an example with four clusters where Bill and Ian are on their own. No wonder, as they are the only two performing well in both English and Algebra.

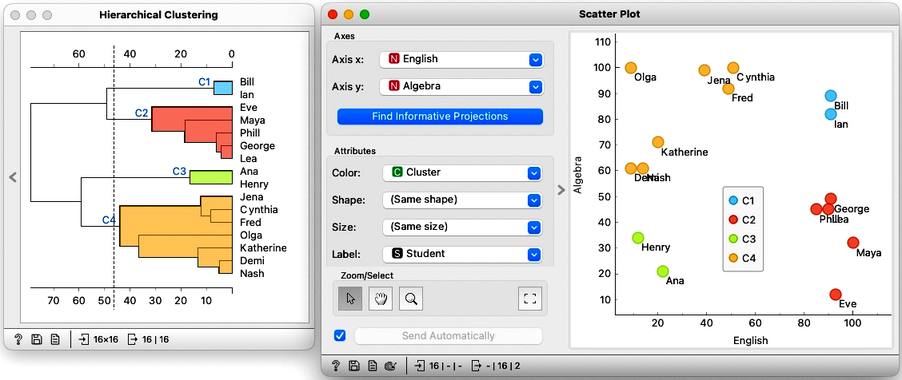
How many clusters are there in our data? Well, this is hard to say. Dendrogram visualizes the clustering structure, and it is usually up to domain experts, in this case, the teachers, to decide what they want. In any case, it is best to select the cut-off for the clustering where the number of clusters would not change under small perturbation of the data. Note, though, that everything we have done so far was on the two-dimensional data. We now need to move to higher number of dimensions.

Chapter 9: High Dimensions

So far we have performed hierarchical clustering in two dimensions. We used the course grades dataset, selecting only the scores in English and Algebra, and visualized them on a scatter plot. There, we developed the concepts of instance distances and distances between clusters. As a refresher: to measure the distance between two students, say, we summed the squared differences between their grades in Algebra and English. We referred to this as the Euclidean distance and noted that it comes from the Pythagorean theorem.

Just as a side note: using Euclidean distance with data with large number of dimensions hits the problem called the curse of dimensionality, where everything becomes similarly far away. We will skip this problem for now and assume Euclidean distance is just fine for any kind of data.

Now what happens if we add another subject, say History? The data would then be in three dimensions. So we would need to extend our Euclidean distance and add the squared difference of grades in History. And, if we add another subject, like Biology, the distance equation gets extended with the squared differences of those grades as well. In this way, we can use Euclidean distance in a space with an arbitrary number of dimensions.

So, what about distances between clusters, that is, linkages? They stay the same as we have defined them for two dimensions as they depend only on the data item distances, which we now know how to compute.

Equipped with this new knowledge, that is, with the idea that Euclidean distance can be used in arbitrary dimensions and that we can used already introduced linkages between clusters, we can now try clustering our entire dataset. We load the grades data in Datasets widget and get the distances between all the pairs of data instances so we can perform our hierarchical clustering. To make sure: we can again use Euclidean distance, and perhaps normalize the features this time. Let us not forget that we need use normalization when variables have different ranges and domains. Now taking a look at the dendrogram we can see that our data may include three clusters.

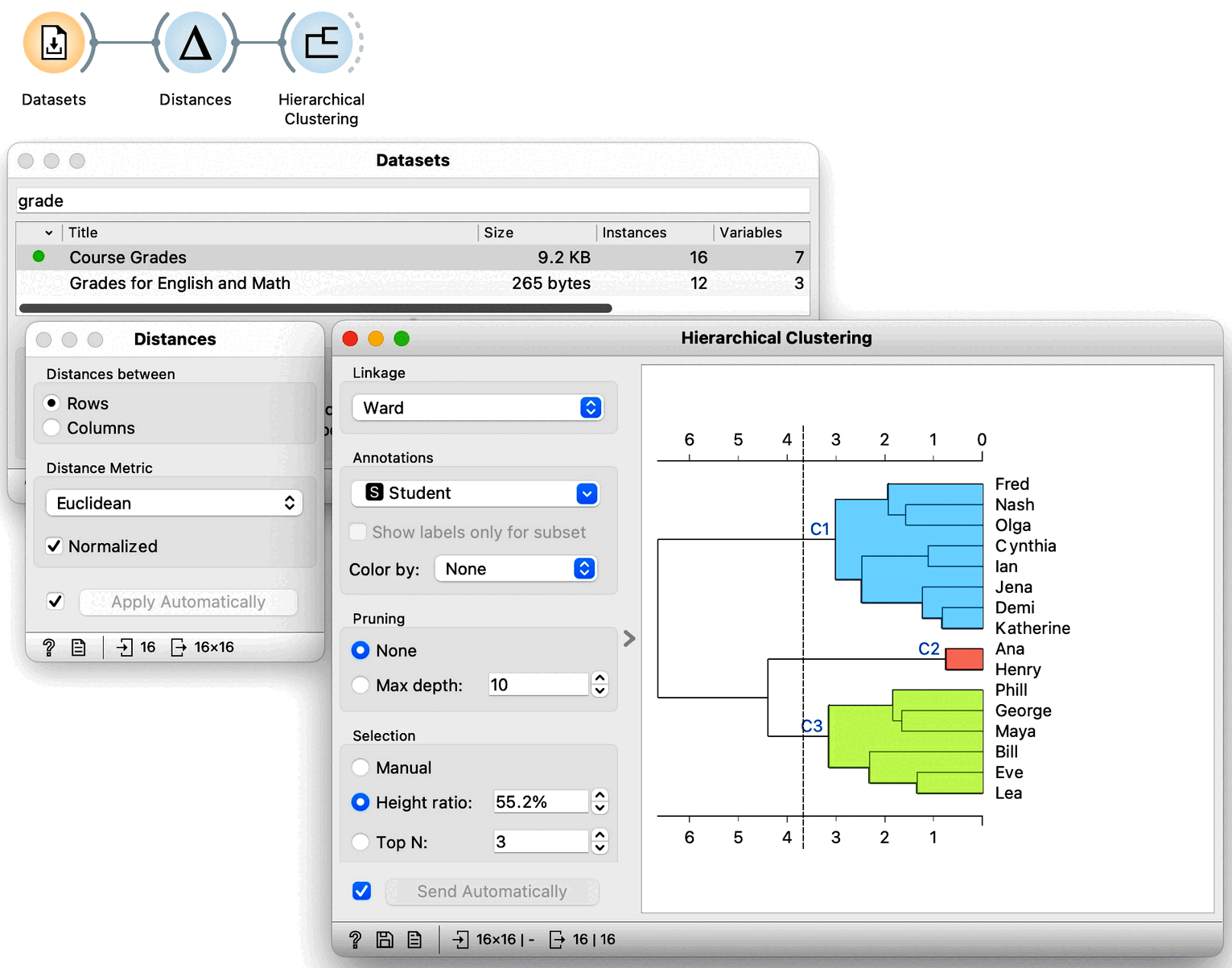
We would now like to get some intuition on what these clusters represent. We could, in principle, use Scatter Plot to try to understand what happened, but now we have seven-dimensional data, and just peeking at two dimensions at a time won’t tell me much. Let us take a quick look anyway by adding a Scatter Plot at the output of Hierarchical Clustering. Here is the data projected onto the Algebra-English plane.

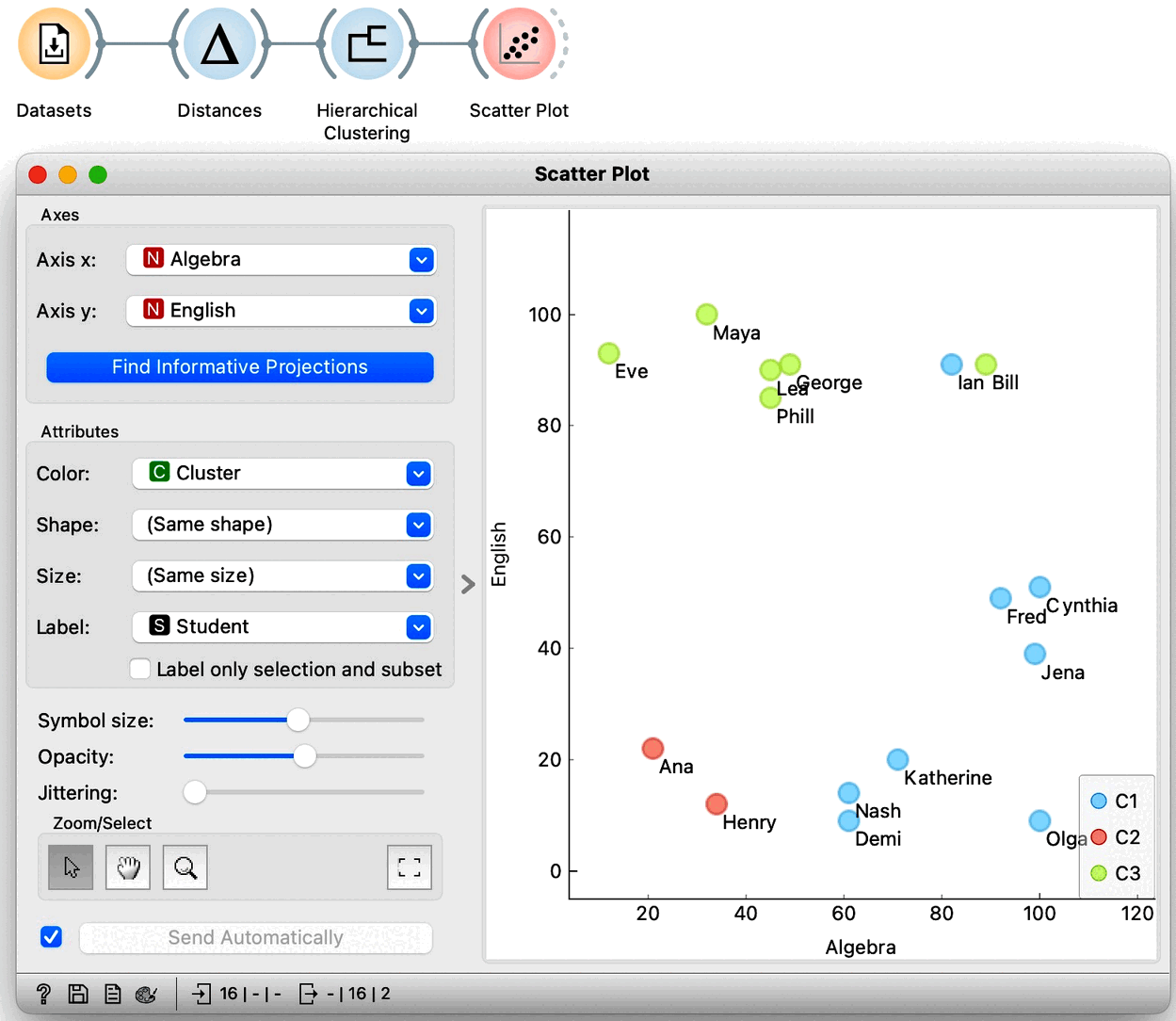
The students with similar grades in these two subjects are indeed in the same cluster. However, we also see Bill and Ian close together but in different clusters. It seems we are going to need a different tool to explain the clusters. Just as a hint: we have already used the widget that we will use for cluster explanation in the section on data distributions. But before we jump to explaining clusters, which is an all-important subject, let us explore the clustering of countries using human development index data. And use geo-maps to visualize the results.